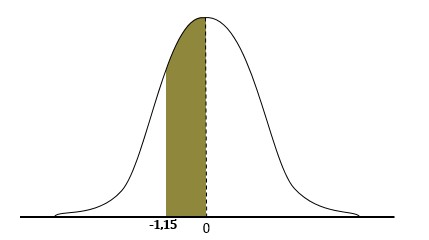
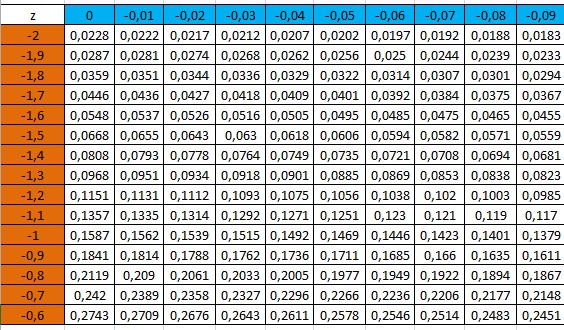
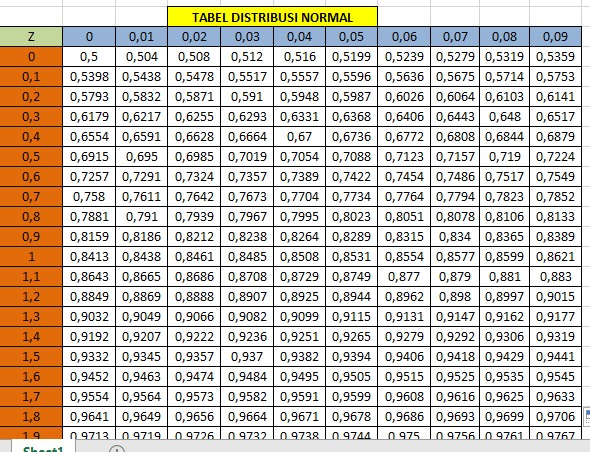
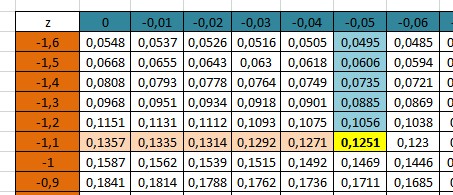
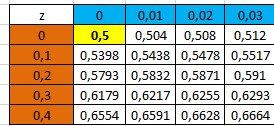
Bank Soal Matematika SMA Distribusi Normal
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
sama dengan ...
Pilih semua jawaban yang benar.
Matematika
Level 4
Bilangan
Pecahan
Bentuk Pecahan
Sebuah segitiga mempunyai tinggi 20 cm dan alas 8 cm. Luas segitiga tersebut adalah ... cm2
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Segitiga
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"

Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra
Complete the gaps with the correct 'to be' in Simple Present Tense.
My mother ... an English teacher and her sisters ... nurses.
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Simple Present Tense
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Kelipatan Bilangan
Jumlah sisi Segitiga + Jumlah sisi Segi Empat adalah ...
Matematika
Level 4
Geometri
Bangun Datar
Segi Banyak
KPK dari bilangan 42 dan 56 adalah ...
Matematika
Level 4
Bilangan
FPB dan KPK
KPK
Timun Mas
Ilustrasi by Cynthia Chandra for kejarcita
Di suatu desa hiduplah seorang janda tua yang bernama Mbok Sarni. Dia tinggal sendirian dan merasa kesepian. Dia sangat mendambakan adanya seorang anak yang bisa menemaninya. Suatu sore, Mbok Sarni pergi ke hutan untuk mencari kayu. Di tengah jalan Mbok Sarni bertemu dengan raksasa pemakan manusia. Ia gemetar ketakutan dan memohon raksasa untuk membiarkannya pergi.
"Baiklah, aku akan melepasmu kalau kau bisa memberiku seorang anak untuk disantap!" gelegar suara raksasa tersebut.
"Tapi aku tidak punya anak!" jawab Mbok Sarni dengan lirih.
"Grrr... kalau begitu, ambil biji mentimun ini! Aku titip untuk kau tanam. Lima belas tahun lagi aku akan kembali untuk memakannya," geram sang raksasa.
Mbok Sarni pun pulang dan menanam biji itu di halaman rumahnya. Setelah dua minggu, mentimun itu tumbuh dan berbuah sangat lebat. Salah satu mentimun terlihat berukuran cukup besar. Mbok Sarni kemudian memetik dan membelahnya. Ternyata mentimun itu berisi seorang bayi yang cantik jelita. Bayi itu kemudian diberi nama Timun Mas.
Walaupun bahagia mendapat seorang anak, Mbok Sarni teringat akan janjinya pada raksasa. Ia berpikir keras mencari cara agar Timun Mas tidak diambil oleh raksasa. Setelah mendengar tentang adanya petapa sakti, ia segera menyuruh Timun Mas untuk pergi meminta pertolongan. Oleh sang petapa, Timun Mas diberi empat buah bungkusan kecil untuk ditaburkan jika ia dikejar raksasa.
Benar saja, ketika saatnya tiba, raksasa datang menagih janjinya. Mbok Sarni berusaha mengulur waktu agar Timun Mas bisa kabur. Menyadari hal itu, si raksasa murka dan segera mengejar Timun Mas. Pertama Timun Mas melemparkan kantong yang berisi biji mentimun. Sungguh ajaib, timbul ladang mentimun yang lebat buahnya. Langkah raksasa pun menjadi terhambat, karena tubuhnya terlilit batang timun. Lalu dari jarum di kantong kedua tumbuhlah pohon-pohon bambu yang sangat tinggi dan tajam. Kemudian, garam dalam kantong ketiga mengubah hutan menjadi lautan yang luas. Namun tetap saja sang raksasa berhasil terbebas dari hambatan dan terus mengejar Timun Mas. Ketakutan, Timun Mas pun melempar kantong terakhirnya yang berisi terasi. Dari situ terbentuklah lautan lumpur yang mendidih. Akhirnya sang raksasa tercebur di dalamnya dan mati. Timun Mas kembali ke rumah Mbok Sarni dengan lega. Mereka pun hidup berbahagia.
(Sumber: stapleskertas.blogspot.com, dengan penyesuaian)
Latar suasana ketika Mbok Sarni bertemu raksasa adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Cerita Rakyat

Sudut pelurus pada gambar di atas yaitu…
Matematika
Level 4
Geometri
Garis dan Sudut
Sudut
Berikut adalah diagram batang nama makanan dan jumlah porsi yang berhasil terjual hari ini di rumah makan Bu Tuni.
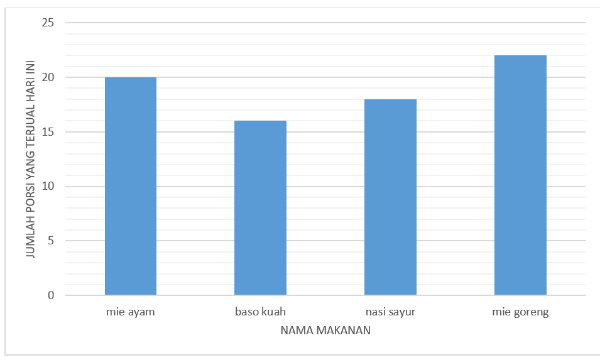
Berapa porsi bakso kuah yang terjual?
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
sama dengan ...
Pilih semua jawaban yang benar.
Sebuah segitiga mempunyai tinggi 20 cm dan alas 8 cm. Luas segitiga tersebut adalah ... cm2
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"
Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....
Complete the gaps with the correct 'to be' in Simple Present Tense.
My mother ... an English teacher and her sisters ... nurses.
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Jumlah sisi Segitiga + Jumlah sisi Segi Empat adalah ...
KPK dari bilangan 42 dan 56 adalah ...
Timun Mas
Ilustrasi by Cynthia Chandra for kejarcita
Di suatu desa hiduplah seorang janda tua yang bernama Mbok Sarni. Dia tinggal sendirian dan merasa kesepian. Dia sangat mendambakan adanya seorang anak yang bisa menemaninya. Suatu sore, Mbok Sarni pergi ke hutan untuk mencari kayu. Di tengah jalan Mbok Sarni bertemu dengan raksasa pemakan manusia. Ia gemetar ketakutan dan memohon raksasa untuk membiarkannya pergi.
"Baiklah, aku akan melepasmu kalau kau bisa memberiku seorang anak untuk disantap!" gelegar suara raksasa tersebut.
"Tapi aku tidak punya anak!" jawab Mbok Sarni dengan lirih.
"Grrr... kalau begitu, ambil biji mentimun ini! Aku titip untuk kau tanam. Lima belas tahun lagi aku akan kembali untuk memakannya," geram sang raksasa.
Mbok Sarni pun pulang dan menanam biji itu di halaman rumahnya. Setelah dua minggu, mentimun itu tumbuh dan berbuah sangat lebat. Salah satu mentimun terlihat berukuran cukup besar. Mbok Sarni kemudian memetik dan membelahnya. Ternyata mentimun itu berisi seorang bayi yang cantik jelita. Bayi itu kemudian diberi nama Timun Mas.
Walaupun bahagia mendapat seorang anak, Mbok Sarni teringat akan janjinya pada raksasa. Ia berpikir keras mencari cara agar Timun Mas tidak diambil oleh raksasa. Setelah mendengar tentang adanya petapa sakti, ia segera menyuruh Timun Mas untuk pergi meminta pertolongan. Oleh sang petapa, Timun Mas diberi empat buah bungkusan kecil untuk ditaburkan jika ia dikejar raksasa.
Benar saja, ketika saatnya tiba, raksasa datang menagih janjinya. Mbok Sarni berusaha mengulur waktu agar Timun Mas bisa kabur. Menyadari hal itu, si raksasa murka dan segera mengejar Timun Mas. Pertama Timun Mas melemparkan kantong yang berisi biji mentimun. Sungguh ajaib, timbul ladang mentimun yang lebat buahnya. Langkah raksasa pun menjadi terhambat, karena tubuhnya terlilit batang timun. Lalu dari jarum di kantong kedua tumbuhlah pohon-pohon bambu yang sangat tinggi dan tajam. Kemudian, garam dalam kantong ketiga mengubah hutan menjadi lautan yang luas. Namun tetap saja sang raksasa berhasil terbebas dari hambatan dan terus mengejar Timun Mas. Ketakutan, Timun Mas pun melempar kantong terakhirnya yang berisi terasi. Dari situ terbentuklah lautan lumpur yang mendidih. Akhirnya sang raksasa tercebur di dalamnya dan mati. Timun Mas kembali ke rumah Mbok Sarni dengan lega. Mereka pun hidup berbahagia.
(Sumber: stapleskertas.blogspot.com, dengan penyesuaian)
Latar suasana ketika Mbok Sarni bertemu raksasa adalah ....
Sudut pelurus pada gambar di atas yaitu…
Berikut adalah diagram batang nama makanan dan jumlah porsi yang berhasil terjual hari ini di rumah makan Bu Tuni.
Berapa porsi bakso kuah yang terjual?