Bank Soal Matematika SMA Konsep Turunan Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Pecahan tersebut senilai dengan pecahan ...
Matematika
Level 4
Bilangan
Pecahan
Pecahan Senilai
Luas sebidang tanah 2,45 ha. Di atas tanah tersebut dibangun 80 kaveling rumah dengan luas masing-masing keveling 180 m2. Kemudian seluas 12,6 are untuk lapangan olahraga. Luas lahan yang belum digunakan ada … m2. (UASBN 2009/2010)
Matematika
Level 4
Geometri
Bangun Datar
Di bawah ini adalah unsur-unsur yang terdapat di dalam sebuah karya sastra, kecuali ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Vocabulary: Jobs
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Kelipatan Bilangan
Rumus keliling persegi yaitu …
Matematika
Level 5,6
Geometri
Bangun Datar
Di sebuah mall terpasang lampu hias. Lampu biru menyala setiap 12 detik, kemudian padam. Lampu merah menyala setiap 16 detik kemudian padam. Lampu kuning menyala setiap 18 detik kemudian padam. maka ketiga lampu akan menyala secara bersamaan pada detik ke ...
Matematika
Level 4
Bilangan
FPB dan KPK
KPK
Cermati teks berikut!
Kancil dan Siput Adu Lari

Pagi itu, kancil berpapasan dengan seekor siput di pinggir sungai. Melihat langkah siput yang sangat lambat, terbitlah rasa sombong sang kancil. "Hei siput, jalanmu lambat sekali! Coba lihat, aku bisa berlari ke ujung jalan di sana dan kembali lagi sebelum kamu selesai satu langkah!" Siput seperti tidak mendengar ujaran sang kancil dan terus berjalan dengan santai. Panas hati sang kancil karena tidak ditanggapi oleh si siput. "Siput bodoh, kamu pasti tidak akan bisa mengalahkanku dalam adu lari!" hina sang kancil.
Tak disangka-sangka, kali ini siput menjawab,"Ayo saja, kita buktikan siapa yang menang adu lari. Kalau aku menang, kamu harus mengaku kalah dan minta maaf kepadaku." Kancil tercengang mendengar keberanian sang siput, lalu menyetujui tantangan itu,"Baik, kalau begitu mari kita adu lari besok pagi di tempat ini juga."
Setelah kancil pergi, siput segera mengumpulkan saudara-saudaranya sesama siput. Ia menjelaskan rencananya untuk mengalahkan sang kancil. Sepanjang sisa hari itu semua siput akan bergerak menempatkan diri di sepanjang sungai, sehingga terdapat seekor siput setiap jarak tertentu. Lalu mereka menunggu di tempatnya masing-masing hingga pertandingan dimulai esok paginya. Beberapa siput sisanya ia tugaskan untuk menyebarkan berita lomba ini ke seluruh hutan.
Waktu pertandingan telah tiba. Banyak hewan hutan telah datang untuk menonton adu lari ini. Dengan tenangnya si siput berujar,"Hai kancil, hewan-hewan hutan akan menjadi saksi pemenang adu lari ini. Bersiap-siaplah untuk mengaku kalah!" Sang kancil jadi merasa gugup karena siput begitu percaya diri.
Begitu tanda mulai diberikan, kancil langsung melesat jauh di depan siput. Ketika kancil mulai merasa lelah, ia berhenti sebentar dengan niat mau beristirahat. Dengan ragu-ragu ia memanggil,"Put, siput?" "Ya, aku di sini," jawab salah satu siput yang berada di dekatnya. Merasa panik, kancil tidak jadi istirahat dan segera lanjut berlari seperti kesurupan. Setelah beberapa kali mendengar jawaban siput seperti itu, ia pun menyerah karena tidak kuat berlari lagi. Seluruh isi hutan pun terkejut dan bersorak sorai melihat kancil mengaku kalah dan meminta maaf pada siput.
Latar waktu dari cerita di atas adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Dongeng
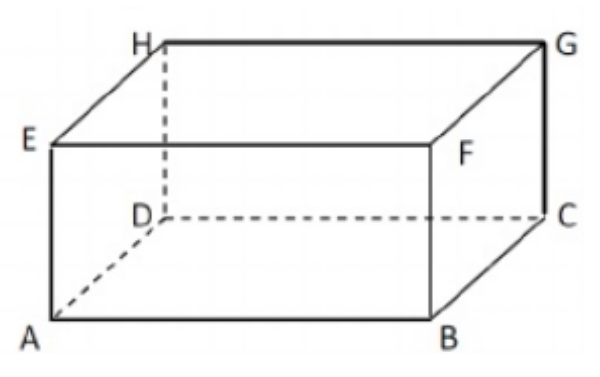
Garis yang sejajar dengan GH adalah ...
Matematika
Level 4
Geometri
Garis dan Sudut
Hubungan Antar Garis
Berikut adalah diagram batang jumlah coklat yang dimakan oleh sebuah keluarga di sebuah pesta.
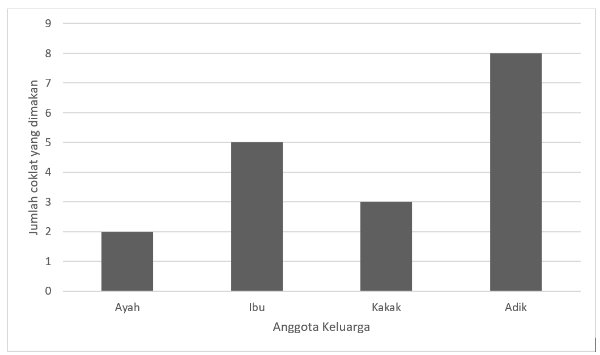
Jumlah coklat yang dimakan Ayah + Ibu ............. jumlah coklat yang dimakan Adik
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pecahan tersebut senilai dengan pecahan ...
Luas sebidang tanah 2,45 ha. Di atas tanah tersebut dibangun 80 kaveling rumah dengan luas masing-masing keveling 180 m2. Kemudian seluas 12,6 are untuk lapangan olahraga. Luas lahan yang belum digunakan ada … m2. (UASBN 2009/2010)
Di bawah ini adalah unsur-unsur yang terdapat di dalam sebuah karya sastra, kecuali ....
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Rumus keliling persegi yaitu …
Di sebuah mall terpasang lampu hias. Lampu biru menyala setiap 12 detik, kemudian padam. Lampu merah menyala setiap 16 detik kemudian padam. Lampu kuning menyala setiap 18 detik kemudian padam. maka ketiga lampu akan menyala secara bersamaan pada detik ke ...
Cermati teks berikut!
Kancil dan Siput Adu Lari
Pagi itu, kancil berpapasan dengan seekor siput di pinggir sungai. Melihat langkah siput yang sangat lambat, terbitlah rasa sombong sang kancil. "Hei siput, jalanmu lambat sekali! Coba lihat, aku bisa berlari ke ujung jalan di sana dan kembali lagi sebelum kamu selesai satu langkah!" Siput seperti tidak mendengar ujaran sang kancil dan terus berjalan dengan santai. Panas hati sang kancil karena tidak ditanggapi oleh si siput. "Siput bodoh, kamu pasti tidak akan bisa mengalahkanku dalam adu lari!" hina sang kancil.
Tak disangka-sangka, kali ini siput menjawab,"Ayo saja, kita buktikan siapa yang menang adu lari. Kalau aku menang, kamu harus mengaku kalah dan minta maaf kepadaku." Kancil tercengang mendengar keberanian sang siput, lalu menyetujui tantangan itu,"Baik, kalau begitu mari kita adu lari besok pagi di tempat ini juga."
Setelah kancil pergi, siput segera mengumpulkan saudara-saudaranya sesama siput. Ia menjelaskan rencananya untuk mengalahkan sang kancil. Sepanjang sisa hari itu semua siput akan bergerak menempatkan diri di sepanjang sungai, sehingga terdapat seekor siput setiap jarak tertentu. Lalu mereka menunggu di tempatnya masing-masing hingga pertandingan dimulai esok paginya. Beberapa siput sisanya ia tugaskan untuk menyebarkan berita lomba ini ke seluruh hutan.
Waktu pertandingan telah tiba. Banyak hewan hutan telah datang untuk menonton adu lari ini. Dengan tenangnya si siput berujar,"Hai kancil, hewan-hewan hutan akan menjadi saksi pemenang adu lari ini. Bersiap-siaplah untuk mengaku kalah!" Sang kancil jadi merasa gugup karena siput begitu percaya diri.
Begitu tanda mulai diberikan, kancil langsung melesat jauh di depan siput. Ketika kancil mulai merasa lelah, ia berhenti sebentar dengan niat mau beristirahat. Dengan ragu-ragu ia memanggil,"Put, siput?" "Ya, aku di sini," jawab salah satu siput yang berada di dekatnya. Merasa panik, kancil tidak jadi istirahat dan segera lanjut berlari seperti kesurupan. Setelah beberapa kali mendengar jawaban siput seperti itu, ia pun menyerah karena tidak kuat berlari lagi. Seluruh isi hutan pun terkejut dan bersorak sorai melihat kancil mengaku kalah dan meminta maaf pada siput.
Latar waktu dari cerita di atas adalah ....
Garis yang sejajar dengan GH adalah ...
Berikut adalah diagram batang jumlah coklat yang dimakan oleh sebuah keluarga di sebuah pesta.
Jumlah coklat yang dimakan Ayah + Ibu ............. jumlah coklat yang dimakan Adik



