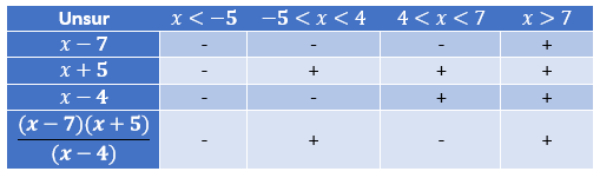
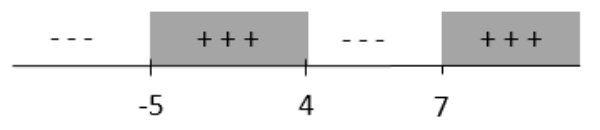
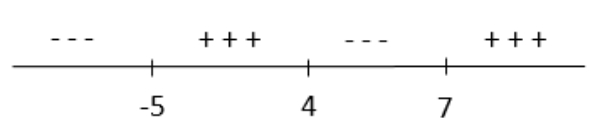Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Pernyataan berikut yang merupakan pertidaksamaan linear satu variabel adalah ...
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Kalimat Benar, Salah, dan Terbuka
73= ...
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
Pak Arif, Pak Bagus, dan Pak Chiko adalah penduduk Desa Bahagia yang pekerjaannya bertani. Pak Arif menanam singkong, padi, dan kentang; Pak Bagus menanam talas, kentang, dan jagung; Pak Chiko menanam singkong dan kentang. Himpunan semua jenis tanaman penduduk Desa Bahagia yang bertani adalah …
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Diketahui sudut U dan sudut V adalah dua sudut yang saling berpelurus. Jika besar sudut U sama dengan bagian dari sudut pelurusnya, maka besar sudut V adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Teks yang menggambarkan keadaan, bentuk atau suasana tertentu adalah ....
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Ciri dan Tujuan Teks Deskripsi
Berikut ini adalah bagian-bagian surat yang hanya terdapat dalam surat dinas, yaitu ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Unsur-unsur dan Kebahasaan Surat
Variabel pada bentuk aljabar adalah ….
(Pilih semua jawaban yang benar!)
Matematika
Level 7
Aljabar
Bentuk Aljabar
Konsep Bentuk Aljabar
Di bawah ini yang termasuk ke dalam contoh buku fiksi adalah ...
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Unsur Pembangun Buku Fiksi dan Nonfiksi
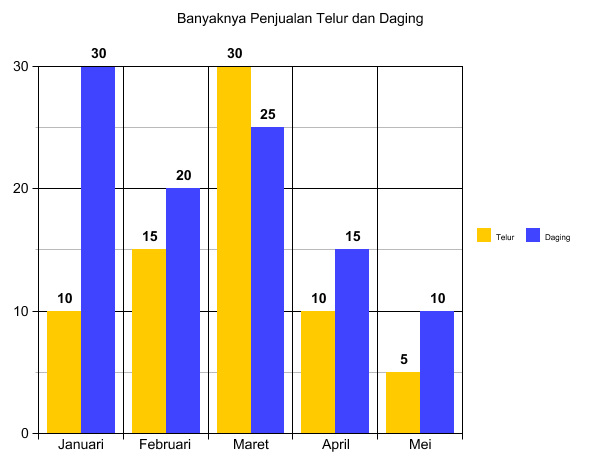
Kenaikan penjualan telur tertinggi terjadi pada bulan ....
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
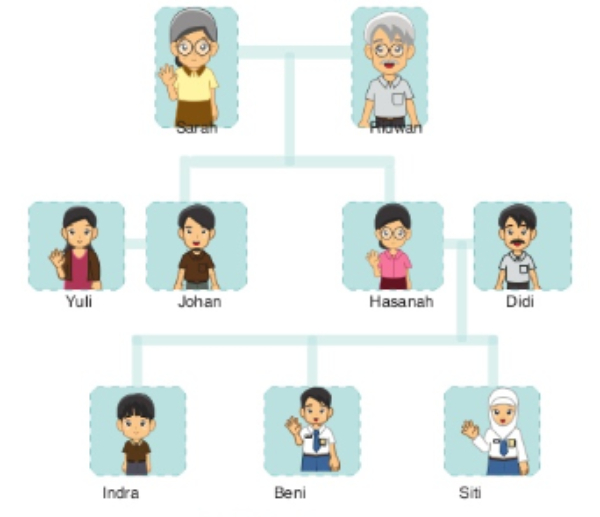
Study the picture of a family tree below.
picture: Buku Bahasa Inggris 'When English Rings a Bell'
Hi, my name is Beni. Above is my family tree. There are nine people in my family. My brother is Indra, and my sister is Siti. My mother is Hasanah, and my father is Didi. I have an uncle and an auntie. They are Johan and Yuli. I also live with my grandparents, Sarah and Ridwan.
Didi is my ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Vocabulary: Family Tree
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pernyataan berikut yang merupakan pertidaksamaan linear satu variabel adalah ...
73= ...
Pak Arif, Pak Bagus, dan Pak Chiko adalah penduduk Desa Bahagia yang pekerjaannya bertani. Pak Arif menanam singkong, padi, dan kentang; Pak Bagus menanam talas, kentang, dan jagung; Pak Chiko menanam singkong dan kentang. Himpunan semua jenis tanaman penduduk Desa Bahagia yang bertani adalah …
Diketahui sudut U dan sudut V adalah dua sudut yang saling berpelurus. Jika besar sudut U sama dengan bagian dari sudut pelurusnya, maka besar sudut V adalah ....
Teks yang menggambarkan keadaan, bentuk atau suasana tertentu adalah ....
Berikut ini adalah bagian-bagian surat yang hanya terdapat dalam surat dinas, yaitu ....
Variabel pada bentuk aljabar adalah ….
(Pilih semua jawaban yang benar!)
Di bawah ini yang termasuk ke dalam contoh buku fiksi adalah ...
Kenaikan penjualan telur tertinggi terjadi pada bulan ....
Study the picture of a family tree below.
picture: Buku Bahasa Inggris 'When English Rings a Bell'
Hi, my name is Beni. Above is my family tree. There are nine people in my family. My brother is Indra, and my sister is Siti. My mother is Hasanah, and my father is Didi. I have an uncle and an auntie. They are Johan and Yuli. I also live with my grandparents, Sarah and Ridwan.
Didi is my ....