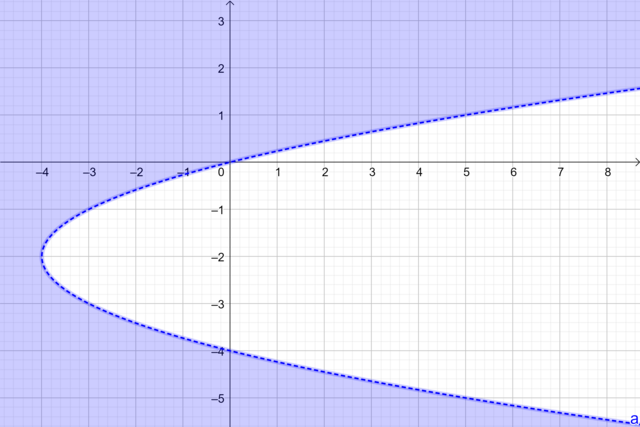
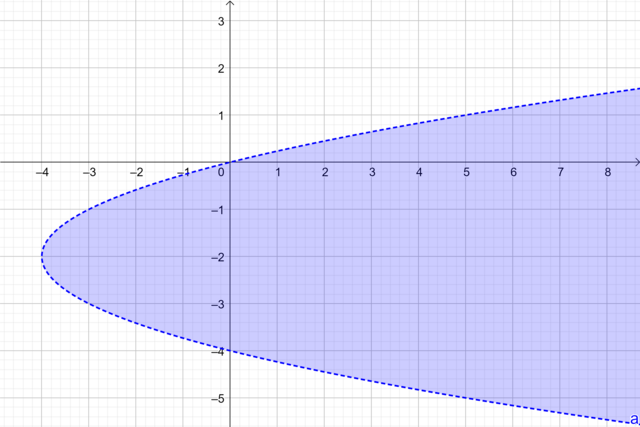
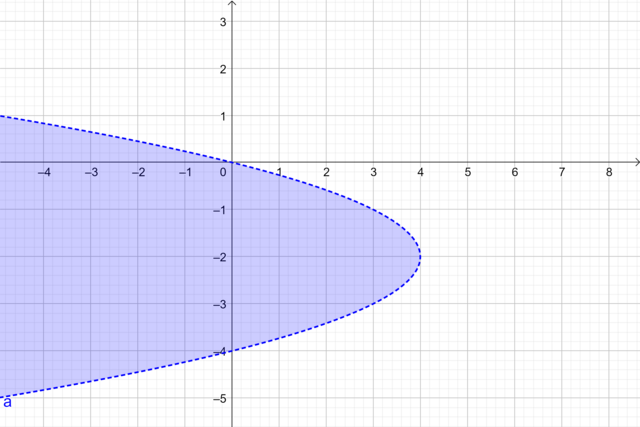
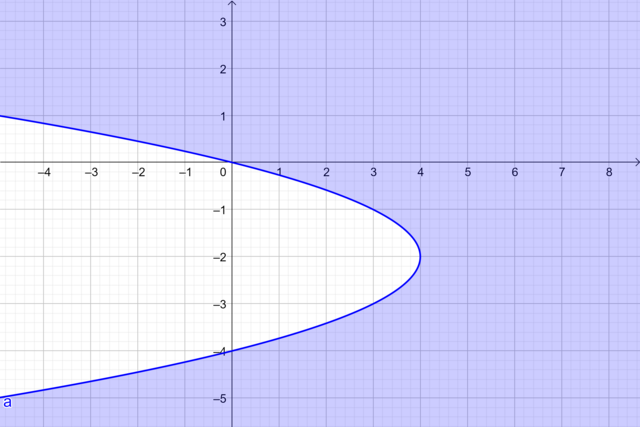
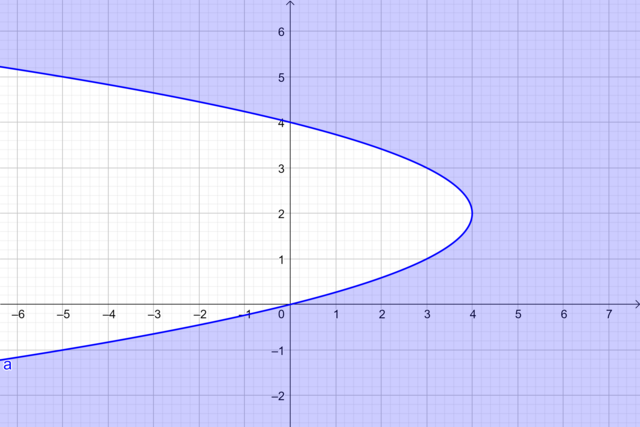
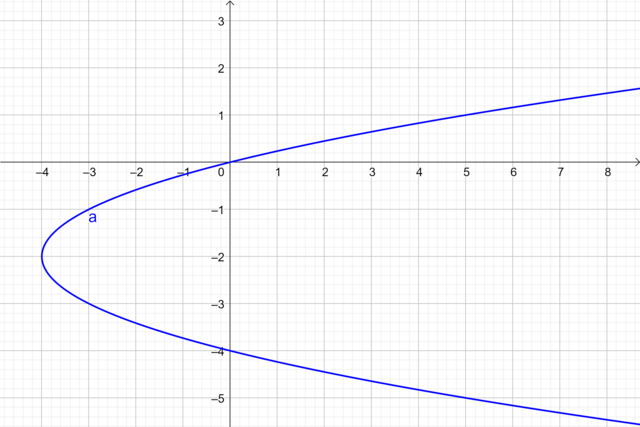
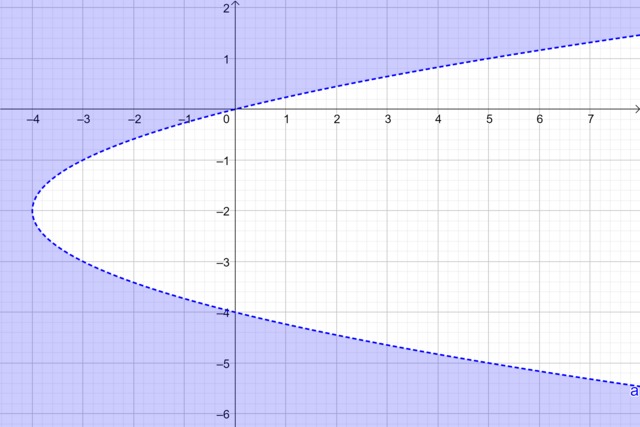
Bank Soal Matematika SMA Pertidaksamaan Dua Variabel
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bilangan 73 ... 102
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Membandingkan dan Mengurutkan Bilangan
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Penolakan

(Sumber: freepik.com)
Perhatikan bangun ruang yang memiliki ciri-ciri sebagai berikut:
1. Memiliki 8 sisi,
2. Memiliki 2 sisi berbentuk segienam dan 6 sisi berbentuk persegi panjang,
3. Memiliki 12 titik sudut,
4. Memiliki 18 rusuk.
Bangun ruang yang memiliki ciri-ciri di atas ditunjukkan oleh bangun ruang yang berbentuk ....
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Rusuk, Sisi, Ruas Garis

(Sumber Gambar: infoperbankan.com)
Perbandingan yang tepat untuk mengisi titik-titik di atas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Nilai Mata Uang
Perhatikan gambar berikut!!

(Sumber Gambar: freepik.com)
Banyaknya segi enam pada gambar di atas ada ... buah.
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Ciri-Ciri Bangun Datar Sederhana
Perhatikan gambar berikut!




(Sumber Gambar: DocPlayer.info)
Pecahan uang yang setara dengan uang pada gambar di atas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Setengah jam sama dengan ... menit.
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Waktu

Source: canva.com
Choose the right word based on the spelling above!
Puisi ditulis dalam bentuk ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Mencermati Isi Puisi
2 ratusan + 1 puluhan + 9 satuan = ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bilangan 73 ... 102
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
(Sumber: freepik.com)
Perhatikan bangun ruang yang memiliki ciri-ciri sebagai berikut:
1. Memiliki 8 sisi,
2. Memiliki 2 sisi berbentuk segienam dan 6 sisi berbentuk persegi panjang,
3. Memiliki 12 titik sudut,
4. Memiliki 18 rusuk.
Bangun ruang yang memiliki ciri-ciri di atas ditunjukkan oleh bangun ruang yang berbentuk ....
(Sumber Gambar: infoperbankan.com)
Perbandingan yang tepat untuk mengisi titik-titik di atas adalah ....
Perhatikan gambar berikut!!
(Sumber Gambar: freepik.com)
Banyaknya segi enam pada gambar di atas ada ... buah.
Perhatikan gambar berikut!
(Sumber Gambar: DocPlayer.info)
Pecahan uang yang setara dengan uang pada gambar di atas adalah ....
Setengah jam sama dengan ... menit.
Source: canva.com
Choose the right word based on the spelling above!
Puisi ditulis dalam bentuk ....
2 ratusan + 1 puluhan + 9 satuan = ....