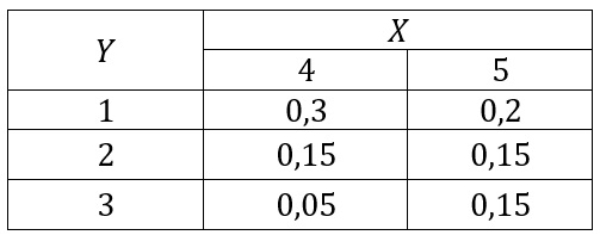
Bank Soal Matematika SMA Distribusi Variabel Acak
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
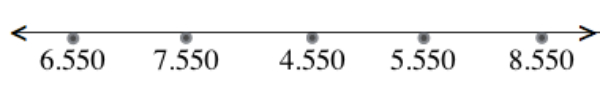
Garis bilangan yang tepat untuk memperbaiki garis bilangan di atas yang menunjukan urutan dari bilangan terkecil hingga bilangan terbesar adalah ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Garis Bilangan (Bilangan Cacah dan Pecahan Sederhana)
Perhatikan gambar berikut.

Kalimat yang sesuai dengan gambar adalah …
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menulis Kalimat Sesuai Gambar
Berikut adalah data hasil penjualan mobil selama beberapa tahun dari suatu toko mobil.
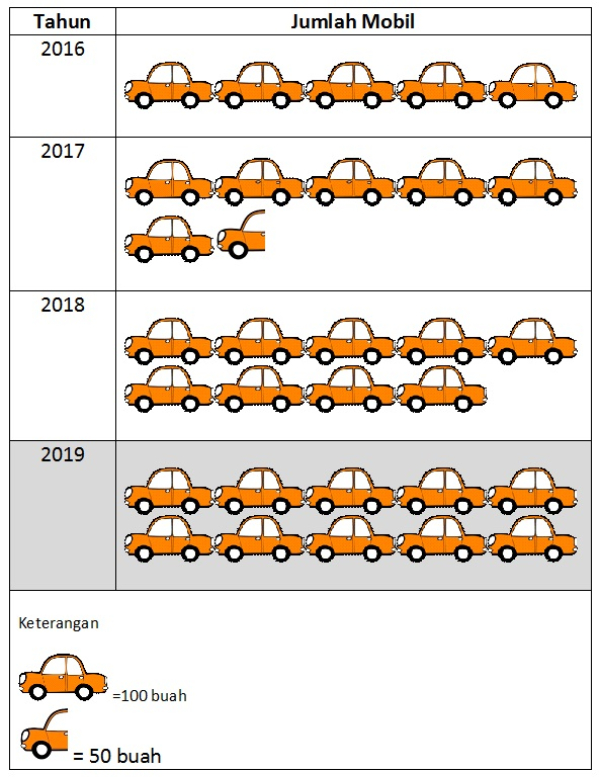
Pernyataan yang sesuai dengan data tersebut adalah ...
Matematika
Level 3
Statistika
Data
Membaca dan Menafsirkan Data
Perhatikan denah berikut!
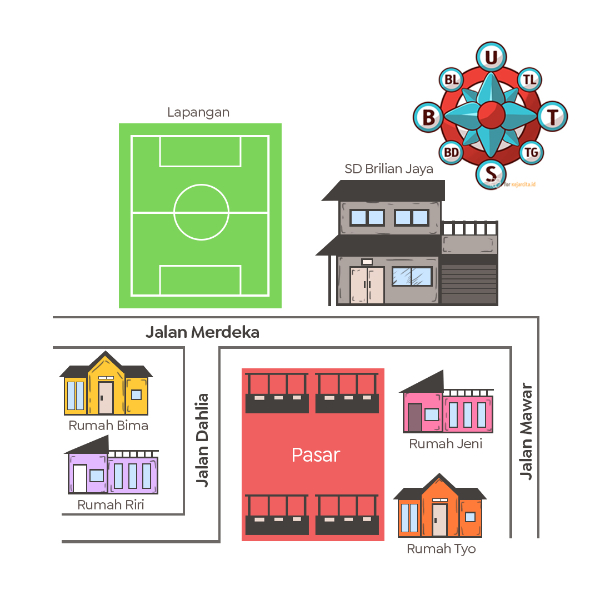
Berikut ini merupakan rumah yang berada di barat daya SD Brilian Jaya adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
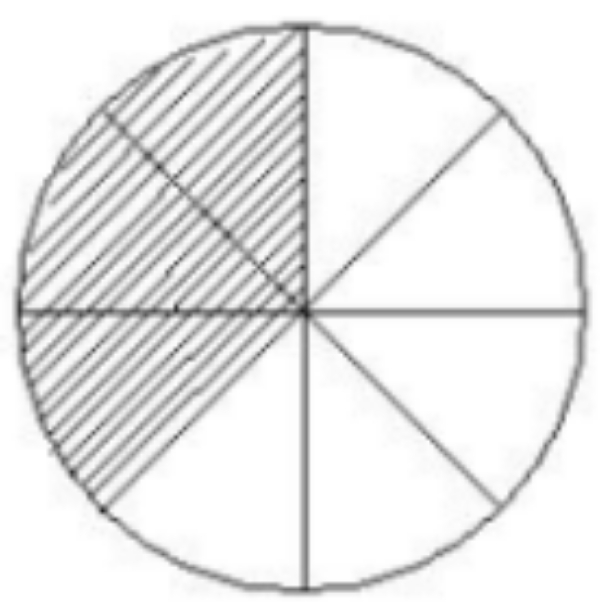
Bagian yang tidak diarsir pada gambar di atas menunjukkan pecahan ...
Matematika
Level 3
Bilangan
Pecahan Sederhana
Menentukan Nilai Pecahan
8 m = ... cm
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Hubungan Antarsatuan Panjang
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
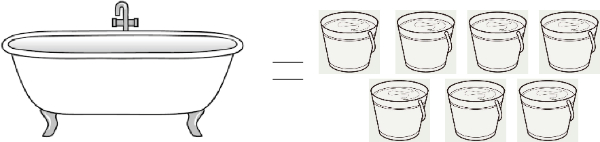
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang
Berikut yang bukan merupakan jenis sudut adalah ....
Matematika
Level 3
Geometri
Bangun Datar
Jenis dan Besar Sudut

Sifat distributif yang benar berada pada kolom ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Sifat-Sifat Operasi Hitung Bilangan Cacah
Perhatikan gambar berikut ini!

Kamu melakukan wawancara dengan orang yang berprofesi seperti gambar di atas. Contoh pertanyaan yang sesuai adalah ...
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menulis Pertanyaan Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Garis bilangan yang tepat untuk memperbaiki garis bilangan di atas yang menunjukan urutan dari bilangan terkecil hingga bilangan terbesar adalah ....
Perhatikan gambar berikut.
Kalimat yang sesuai dengan gambar adalah …
Berikut adalah data hasil penjualan mobil selama beberapa tahun dari suatu toko mobil.
Pernyataan yang sesuai dengan data tersebut adalah ...
Perhatikan denah berikut!
Berikut ini merupakan rumah yang berada di barat daya SD Brilian Jaya adalah ....
Bagian yang tidak diarsir pada gambar di atas menunjukkan pecahan ...
8 m = ... cm
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Berikut yang bukan merupakan jenis sudut adalah ....
Sifat distributif yang benar berada pada kolom ….
Perhatikan gambar berikut ini!
Kamu melakukan wawancara dengan orang yang berprofesi seperti gambar di atas. Contoh pertanyaan yang sesuai adalah ...