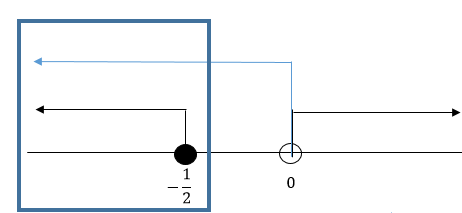
Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
The true statement according to the dialogue above is ...
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting
Metode ilmiah dibangun atas dasar sikap ilmiah dan menghasilkan produk yang tersusun atas tiga komponen terpenting yang berlaku secara universal. Di dalam komponen-komponen tersebut diuraikan lagi mengenai produk fisika. Apa saja produk fisika tersebut?
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Hakikat dan Peran Fisika
Berikut merupakan komponen biotik ekosistem pantai pasir, kecuali ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
Sesuai dengan definisi nilai mutlak, maka nilai dari dan adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Konsep Nilai Mutlak
Penulisan huruf kapital yang salah terdapat pada kalimat …
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Menulis Teks Laporan Hasil Observasi
Organisme yang jumlahnya paling banyak berdasarkan piramida jumlah di bawah ini adalah ....

sumber: amongguru.com
Biologi
Level 10
Biologi
Ekologi
Aliran Energi dan Piramida Ekologi
Perhatikan jenis virus berikut!
- Virus rabies
- Bakteriofag
- Virus flu burung
- Human Immunodeficiency Virus
Dari daftar di atas, virus yang memiliki kisaran inang yang cukup luas adalah ....
Biologi
Level 10
Biologi
Virus
Cara Hidup dan Reproduksi Virus
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Pertidaksamaan yang tepat berdasarkan daerah penyelesaian di bawah ini adalah ....

Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Pertidaksamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
The true statement according to the dialogue above is ...
Metode ilmiah dibangun atas dasar sikap ilmiah dan menghasilkan produk yang tersusun atas tiga komponen terpenting yang berlaku secara universal. Di dalam komponen-komponen tersebut diuraikan lagi mengenai produk fisika. Apa saja produk fisika tersebut?
Berikut merupakan komponen biotik ekosistem pantai pasir, kecuali ....
Sesuai dengan definisi nilai mutlak, maka nilai dari dan adalah ....
Penulisan huruf kapital yang salah terdapat pada kalimat …
Organisme yang jumlahnya paling banyak berdasarkan piramida jumlah di bawah ini adalah ....

sumber: amongguru.com
Perhatikan jenis virus berikut!
- Virus rabies
- Bakteriofag
- Virus flu burung
- Human Immunodeficiency Virus
Dari daftar di atas, virus yang memiliki kisaran inang yang cukup luas adalah ....
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....
Pertidaksamaan yang tepat berdasarkan daerah penyelesaian di bawah ini adalah ....