Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Di bawah ini yang merupakan kalimat tertutup adalah …
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Kalimat Benar, Salah, dan Terbuka
73= ...
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
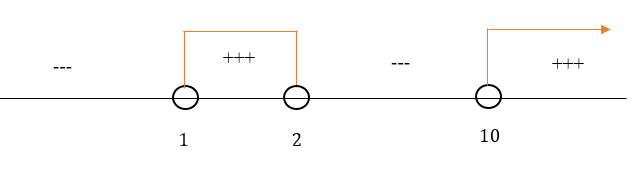
Perhatikan gambar berikut.

Bagian yang diarsir menunjukkan …
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Perhatikan gambar berikut!
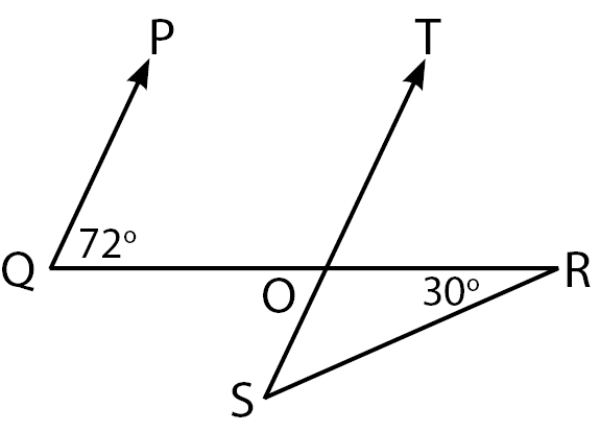
Besar RSO yang memenuhi gambar di atas adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Perhatikan teks berikut!
Roni membeli sebuah hadiah yang diperuntukkan kepada adiknya. Hadiah tersebut dibungkus, dengan sangat rapih dengan kertas kado bermotif bunga-bunga berwarna-warni. Diatas bungkus kado tersebut ditambahkan sebuah pita kecil. Adik Roni merasa begitu bahagianya saat menerima hadiah dari Kakaknya.
Perbaiki teks deskripsi di atas sehingga menjadi kalimat yang efektif!
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Struktur dan Kebahasaan Teks Deskripsi
Surat dinas adalah surat ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Ciri Surat Pribadi dan Surat Dinas
Variabel pada bentuk aljabar adalah ….
(Pilih semua jawaban yang benar!)
Matematika
Level 7
Aljabar
Bentuk Aljabar
Konsep Bentuk Aljabar
Ide pengembangan buku nonfiksi berdasarkan ....
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Unsur Pembangun Buku Fiksi dan Nonfiksi
Tabel di bawah ini memperlihatkan data kegiatan ekstrakurikuler di SMP Merdeka pada tahun 2020.
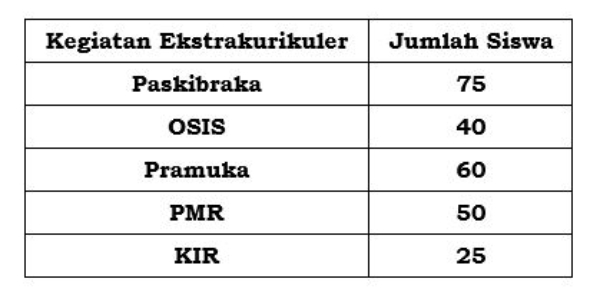
Diagram lingkaran dari tabel tersebut adalah ....
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
Study the picture of a family tree below.
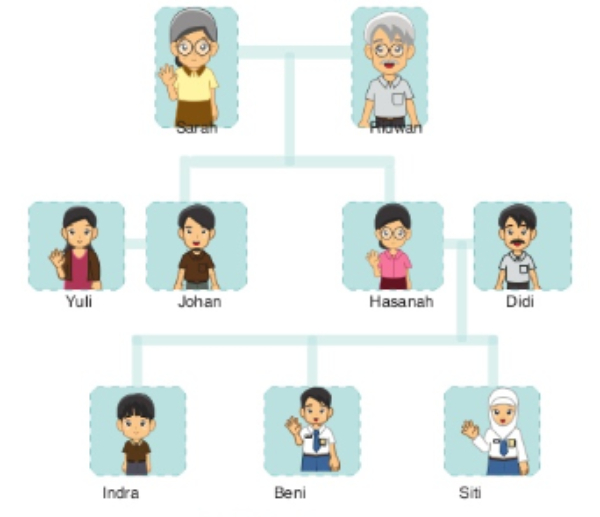
picture: Buku Bahasa Inggris 'When English Rings a Bell'
Hi, my name is Beni. Above is my family tree. There are nine people in my family. My brother is Indra, and my sister is Siti. My mother is Hasanah, and my father is Didi. I have an uncle and an auntie. They are Johan and Yuli. I also live with my grandparents, Sarah and Ridwan.
Didi is my ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Vocabulary: Family Tree
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Di bawah ini yang merupakan kalimat tertutup adalah …
73= ...
Perhatikan gambar berikut.
Bagian yang diarsir menunjukkan …
Perhatikan gambar berikut!
Besar RSO yang memenuhi gambar di atas adalah ....
Perhatikan teks berikut!
Roni membeli sebuah hadiah yang diperuntukkan kepada adiknya. Hadiah tersebut dibungkus, dengan sangat rapih dengan kertas kado bermotif bunga-bunga berwarna-warni. Diatas bungkus kado tersebut ditambahkan sebuah pita kecil. Adik Roni merasa begitu bahagianya saat menerima hadiah dari Kakaknya.
Perbaiki teks deskripsi di atas sehingga menjadi kalimat yang efektif!
Surat dinas adalah surat ....
Variabel pada bentuk aljabar adalah ….
(Pilih semua jawaban yang benar!)
Ide pengembangan buku nonfiksi berdasarkan ....
Tabel di bawah ini memperlihatkan data kegiatan ekstrakurikuler di SMP Merdeka pada tahun 2020.
Diagram lingkaran dari tabel tersebut adalah ....
Study the picture of a family tree below.
picture: Buku Bahasa Inggris 'When English Rings a Bell'
Hi, my name is Beni. Above is my family tree. There are nine people in my family. My brother is Indra, and my sister is Siti. My mother is Hasanah, and my father is Didi. I have an uncle and an auntie. They are Johan and Yuli. I also live with my grandparents, Sarah and Ridwan.
Didi is my ....