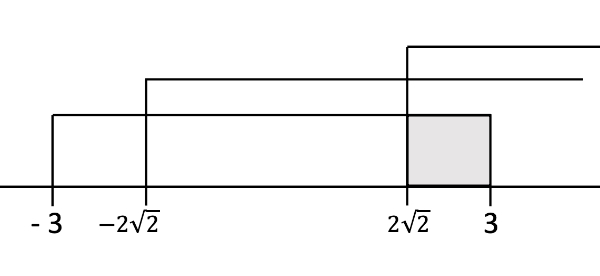
Bank Soal Matematika SMA Pertidaksamaan Logaritma
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
How to Plant Onions
Start with your seeds. Transplant them into larger cells and before planting out, harden them off by putting the pots outside for several days.
In the garden, onion plants should be spaced 4 to 6 inches apart in the row, with rows 1 to 2 feet apart. Plant each one about 1/2 inch deep in a small hole.
After planting, trim the tops to about 4 inches. Onions need about 1 inch of water per week, so if the weather is dry, you’ll need to water them.
(source: www.finegardening.com)
Based on the text above, the writer's intention is to inform readers about a method for ....
Bahasa Inggris
Level 9
Bahasa Inggris
How to do or make things
Procedure Text

Source: mostlybrightideas.wordpress.com
Arrange these jumbled words into a good Passive Voice.
1. opened - long - this - can't - be - door - a - time - for.
2. the - should - to cross - children - be - helped - street.
3. party - Paula's - he - not - invited - might - be - to.
4. the - book - this - library - be - must - soon - returned - to.
What is the best arrangement for point 1?
Bahasa Inggris
Level 9
Bahasa Inggris
Using passive voice to describe things
Passive Voice
Cermati Teks Berikut!
Zat-zat makanan disebut juga gizi atau nutrisi. Makanan bergizi adalah makanan yang mengandung karbohidrat, protein, lemak (lipid), vitamin, dan mineral dalam jumlah yang mencukupi kebutuhan tubuh. Karbohidrat, protein, lemak diperlukan oleh tubuh dalam jumlah banyak sehingga disebut makronutrien. Sementara itu, vitamin dan mineral diperlukan oleh tubuh dalam jumlah yang sedikit sehingga disebut mikronutrien.
Karbohidrat berasal paling banyak pada tumbuh-tumbuhan yang melakukan fotosintesis. Karbohidrat dalam makanan berupa pati, sukrosa, laktosa, dan fruktosa. Lemak tersusun dari atom karbon, hidrogen, dan oksigen. Lemak terdiri atas gliserol dengan asam-asam lemak. Daging dan berbagai produk olahan susu mengandung asam lemak jenuh, sedangkan biji tanaman mengandung asam lemak tak jenuh. Protein tersusun dari atom karbon, hidrogen, oksigen, dan nitrogen. Pada beberapa jenis protein terdapat unsur-unsur mineral sulfur, fosfor, iodin, besi, dan kobalt. Sumber protein berasal dari daging berwarna merah, ikan, telur, susu, kerang, keju, dan kacang-kacangan.
(Sumber: academia.edu-Laporan Uji Zat Makanan, dengan penyesuaian)
Berdasarkan isinya, kutipan tersebut termasuk unsur teks laporan percobaan pada bagian ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
Nilai dari adalah...
Matematika
Level 9
Bilangan
Bilangan Berpangkat dan Bentuk Akar
Bilangan Berpangkat
Tujuan dibuatnya teks diskusi adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
Enzim amilase bekerja memecah tepung menjadi maltosa, selanjutnya maltosa dihidrolisis oleh maltase menjadi glukosa.
Kata ilmiah bercetak miring mempunyai arti ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Struktur dan Kebahasaan Laporan Percobaan
Read the following dialog and answer the question.
Narnia : Hey, Judith. Guess what? My article will be published in The MOST magazine this month!
Judith : Wow, what a great achievement! That's cool, Narnia.
Narnia : Thank you. I've worked so hard to write this special article.
Judith : I know it. I can't wait to read your article published in that magazine. I'm sure I'll buy it.
Narnia : Thank you.
The exclamative expression of congratulating that is presented in the dialog is ...
Bahasa Inggris
Level 9
Bahasa Inggris
Appreciation over achievements or happiness
Expressions of Congratulations
Perbedaan teks diskusi dengan teks eksposisi adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
Baca teks berikut ini dengan cermat.
Pak Kinong, Penggagas Bemo Baca
Sutino adalah seorang pria berusia 58 tahun yang berprofesi sebagai sopir bemo. Pria yang akrab disapa Pak Kinong tersebut sudah bekerja sebagai sopir bemo sejak tahun 1976. Ia berkeliling mencari penumpang di gang-gang sempit di kawasan Tanah Abang. Selain itu, Pak Kinong juga sering keliling di kawasan Kota Tua hingga Jakarta Utara.
Suatu hari, dua teman Pak Kinong yang berprofesi sebagai dosen di Universitas Tarumanegara mendatanginya ingin membeli bemonya. Kedua dosen tersebut ingin mengadakan program Netling (internet keliling). Namun Pak Kinong tidak paham tentang program Netling tersebut. Pak Kinong justru teringat dengan kebiasaan anak-anak sekarang yang sering ia temui ketika berkeliling. Ia prihatin dengan minat baca anak-anak sekarang yang rendah.
Berangkat dari keresahan tersebut, Pak Kinong kemudian mengusulkan kepada dua temannya untuk membuat mobil baca atau perpustakaan keliling. Harapan Pak Kinong, mobil baca tersebut bisa memantik dan memfasilitasi minat baca anak-anak sekarang. Kedua temannya setuju dengan gagasan Pak Kinong.
Mengendarai bemo bacanya, Pak Kinong berkeliling ke sekolah-sekolah seperti PAUD, TK, dan SD yang berada di gang-gang sempit setiap hari pada pukul 09.00 hingga 15.00. Sebelum berkeliling dengan bemo bacanya, ia menjalani rutinitasnya menjadi sopir bemo terlebih dahulu. Rutinitas tersebut ia lakukan sejak tahun 2013 hingga pertengahan 2017.
Gagasan dan inisiatif Pak Kinong melalui bemo bacanya berhasil menarik perhatian publik. Banyak anak muda, terutama mahasiswa, yang kagum dengan tindakan Pak Kinong. Bahkan Presiden Joko Widodo menunjukkan apresiasinya dengan mengundangnya ke Istana Negara pada peringatan Hari Pendidikan Nasional, 2 Mei 2017. Yang lebih mengejutkan lagi ialah hadiah sebuah tiket umroh yang diberikan oleh presiden kepada Pak Kinong. Selain itu, beberapa media juga mengundang Pak Kinong untuk menjadi narasumber tentang perjuangannya menumbuhkan minat baca.
Meski tak pernah merasakan bangku sekolah hingga jenjang perguruan tinggi, Pak Kinong tetap ingin bermanfaat bagi orang lain, terutama dalam dunia pendidikan. Ia berharap anak-anak Indonesia gemar membaca melaui ide kecil bersama bemo bacanya. Baginya, menjadi sesuatu yang sangat disayangkan jika di era yang serba canggih ini minat baca anak-anak malah rendah. Pak Kinong sadar betul, dengan gemar membaca anak-anak akan menjadi pintar dan sukses.
(Sumber: Kompas.com, dengan penyesuaian)
Simpulan yang tepat dari cerita inspiratif di atas adalah ...
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Ide mengumpulkan sampah plastik yang Parmita dan Mazin jalankan berawal dari ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
How to Plant Onions
Start with your seeds. Transplant them into larger cells and before planting out, harden them off by putting the pots outside for several days.
In the garden, onion plants should be spaced 4 to 6 inches apart in the row, with rows 1 to 2 feet apart. Plant each one about 1/2 inch deep in a small hole.
After planting, trim the tops to about 4 inches. Onions need about 1 inch of water per week, so if the weather is dry, you’ll need to water them.
(source: www.finegardening.com)
Based on the text above, the writer's intention is to inform readers about a method for ....
Source: mostlybrightideas.wordpress.com
Arrange these jumbled words into a good Passive Voice.
1. opened - long - this - can't - be - door - a - time - for.
2. the - should - to cross - children - be - helped - street.
3. party - Paula's - he - not - invited - might - be - to.
4. the - book - this - library - be - must - soon - returned - to.
What is the best arrangement for point 1?
Cermati Teks Berikut!
Zat-zat makanan disebut juga gizi atau nutrisi. Makanan bergizi adalah makanan yang mengandung karbohidrat, protein, lemak (lipid), vitamin, dan mineral dalam jumlah yang mencukupi kebutuhan tubuh. Karbohidrat, protein, lemak diperlukan oleh tubuh dalam jumlah banyak sehingga disebut makronutrien. Sementara itu, vitamin dan mineral diperlukan oleh tubuh dalam jumlah yang sedikit sehingga disebut mikronutrien.
Karbohidrat berasal paling banyak pada tumbuh-tumbuhan yang melakukan fotosintesis. Karbohidrat dalam makanan berupa pati, sukrosa, laktosa, dan fruktosa. Lemak tersusun dari atom karbon, hidrogen, dan oksigen. Lemak terdiri atas gliserol dengan asam-asam lemak. Daging dan berbagai produk olahan susu mengandung asam lemak jenuh, sedangkan biji tanaman mengandung asam lemak tak jenuh. Protein tersusun dari atom karbon, hidrogen, oksigen, dan nitrogen. Pada beberapa jenis protein terdapat unsur-unsur mineral sulfur, fosfor, iodin, besi, dan kobalt. Sumber protein berasal dari daging berwarna merah, ikan, telur, susu, kerang, keju, dan kacang-kacangan.
(Sumber: academia.edu-Laporan Uji Zat Makanan, dengan penyesuaian)
Berdasarkan isinya, kutipan tersebut termasuk unsur teks laporan percobaan pada bagian ....
Nilai dari adalah...
Tujuan dibuatnya teks diskusi adalah ....
Enzim amilase bekerja memecah tepung menjadi maltosa, selanjutnya maltosa dihidrolisis oleh maltase menjadi glukosa.
Kata ilmiah bercetak miring mempunyai arti ....
Read the following dialog and answer the question.
Narnia : Hey, Judith. Guess what? My article will be published in The MOST magazine this month! Judith : Wow, what a great achievement! That's cool, Narnia. Narnia : Thank you. I've worked so hard to write this special article. Judith : I know it. I can't wait to read your article published in that magazine. I'm sure I'll buy it. Narnia : Thank you.
The exclamative expression of congratulating that is presented in the dialog is ...
Perbedaan teks diskusi dengan teks eksposisi adalah ....
Baca teks berikut ini dengan cermat.
Pak Kinong, Penggagas Bemo Baca
Sutino adalah seorang pria berusia 58 tahun yang berprofesi sebagai sopir bemo. Pria yang akrab disapa Pak Kinong tersebut sudah bekerja sebagai sopir bemo sejak tahun 1976. Ia berkeliling mencari penumpang di gang-gang sempit di kawasan Tanah Abang. Selain itu, Pak Kinong juga sering keliling di kawasan Kota Tua hingga Jakarta Utara.
Suatu hari, dua teman Pak Kinong yang berprofesi sebagai dosen di Universitas Tarumanegara mendatanginya ingin membeli bemonya. Kedua dosen tersebut ingin mengadakan program Netling (internet keliling). Namun Pak Kinong tidak paham tentang program Netling tersebut. Pak Kinong justru teringat dengan kebiasaan anak-anak sekarang yang sering ia temui ketika berkeliling. Ia prihatin dengan minat baca anak-anak sekarang yang rendah.
Berangkat dari keresahan tersebut, Pak Kinong kemudian mengusulkan kepada dua temannya untuk membuat mobil baca atau perpustakaan keliling. Harapan Pak Kinong, mobil baca tersebut bisa memantik dan memfasilitasi minat baca anak-anak sekarang. Kedua temannya setuju dengan gagasan Pak Kinong.
Mengendarai bemo bacanya, Pak Kinong berkeliling ke sekolah-sekolah seperti PAUD, TK, dan SD yang berada di gang-gang sempit setiap hari pada pukul 09.00 hingga 15.00. Sebelum berkeliling dengan bemo bacanya, ia menjalani rutinitasnya menjadi sopir bemo terlebih dahulu. Rutinitas tersebut ia lakukan sejak tahun 2013 hingga pertengahan 2017.
Gagasan dan inisiatif Pak Kinong melalui bemo bacanya berhasil menarik perhatian publik. Banyak anak muda, terutama mahasiswa, yang kagum dengan tindakan Pak Kinong. Bahkan Presiden Joko Widodo menunjukkan apresiasinya dengan mengundangnya ke Istana Negara pada peringatan Hari Pendidikan Nasional, 2 Mei 2017. Yang lebih mengejutkan lagi ialah hadiah sebuah tiket umroh yang diberikan oleh presiden kepada Pak Kinong. Selain itu, beberapa media juga mengundang Pak Kinong untuk menjadi narasumber tentang perjuangannya menumbuhkan minat baca.
Meski tak pernah merasakan bangku sekolah hingga jenjang perguruan tinggi, Pak Kinong tetap ingin bermanfaat bagi orang lain, terutama dalam dunia pendidikan. Ia berharap anak-anak Indonesia gemar membaca melaui ide kecil bersama bemo bacanya. Baginya, menjadi sesuatu yang sangat disayangkan jika di era yang serba canggih ini minat baca anak-anak malah rendah. Pak Kinong sadar betul, dengan gemar membaca anak-anak akan menjadi pintar dan sukses.
(Sumber: Kompas.com, dengan penyesuaian)
Simpulan yang tepat dari cerita inspiratif di atas adalah ...
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Ide mengumpulkan sampah plastik yang Parmita dan Mazin jalankan berawal dari ....