Bank Soal Matematika SMA Limit Fungsi Aljabar
Soal
Menentukan Nilai Limit Fungsi Matematika Wajib LOTS Teknik Hitung
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bilangan 73 ... 102
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Membandingkan dan Mengurutkan Bilangan
Mengenal Bilangan Cacah (500)
Kelas II
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut ini!

Ungkapan ajakan yang sesuai dengan gambar di atas adalah ...
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Ajakan
Perhatikan bangun ruang di bawah ini.
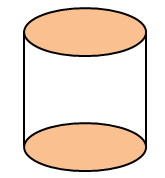
Ciri-ciri yang tepat untuk bangun ruang tersebut adalah ....
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Ciri-Ciri Bangun Ruang Sederhana
Kelas II
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!
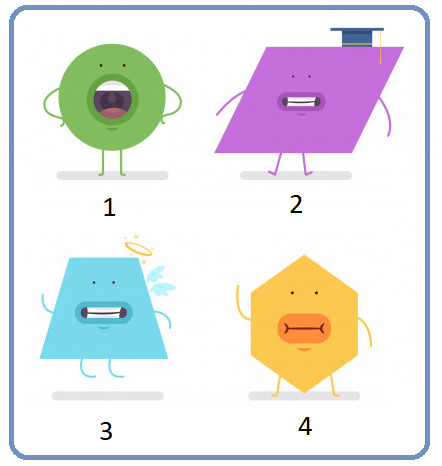
(Sumber Gambar: freepik.com)
Bangun datar yang memiliki jumlah titik sudut yang sama ditunjukkan oleh gambar nomor ....
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Sisi, Sudut, dan Titik Sudut
Kelas II
Kurikulum 2013
K13
Matematika
Pecahan mata uang berikut yang dibaca dua puluh ribu rupiah adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Nilai Mata Uang
Kelas II
Kurikulum 2013
K13
Matematika
Setengah jam sama dengan ... menit.
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Waktu
Kelas II
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!

(Sumber Gambar: id.wikipedia.org)
Kumpulan pecahan mata uang yang nilainya setara dengan gambar di atas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Kelas II
Kurikulum 2013
K13
Matematika
Fill in the blanks.
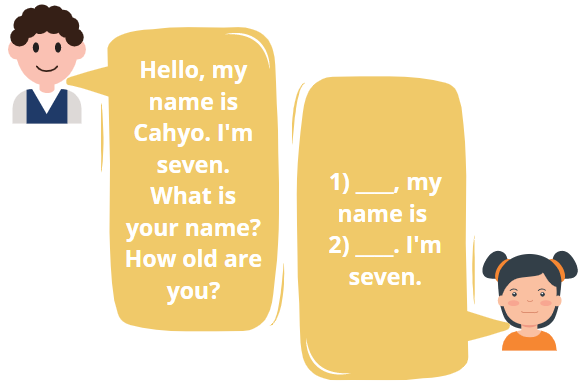
Source: canva
Number 2 is ______.
Bahasa Inggris
Level 2
A NEW FRIEND
Greetings and Spelling
Kelas II
Kurikulum 2013
K13
Bahasa Inggris

(Templat gambar: canva.com)
Arti kata berseri pada puisi di atas adalah ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Mencermati Isi Puisi
Bilangan 331 terdiri dari ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Kelas II
Kurikulum 2013
K13
Matematika
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bilangan 73 ... 102
Perhatikan gambar berikut ini!
Ungkapan ajakan yang sesuai dengan gambar di atas adalah ...
Perhatikan bangun ruang di bawah ini.
Ciri-ciri yang tepat untuk bangun ruang tersebut adalah ....
Perhatikan gambar berikut!
(Sumber Gambar: freepik.com)
Bangun datar yang memiliki jumlah titik sudut yang sama ditunjukkan oleh gambar nomor ....
Pecahan mata uang berikut yang dibaca dua puluh ribu rupiah adalah ....
Setengah jam sama dengan ... menit.
Perhatikan gambar berikut!
(Sumber Gambar: id.wikipedia.org)
Kumpulan pecahan mata uang yang nilainya setara dengan gambar di atas adalah ....
Fill in the blanks.
Source: canva
Number 2 is ______.
(Templat gambar: canva.com)
Arti kata berseri pada puisi di atas adalah ....
Bilangan 331 terdiri dari ....



