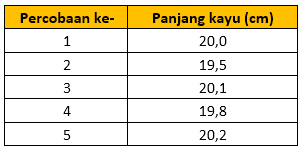
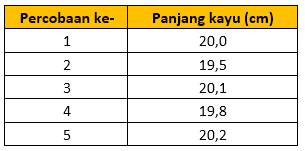
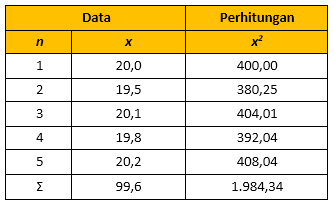
Bank Soal Fisika SMA Pengukuran
Soal
Soal Populer Hari Ini
Pecahan yang senilai dengan pecahan di atas adalah ...
Matematika
Level 4
Bilangan
Pecahan
Pecahan Senilai
Kelas IV
Kurikulum 2013
K13
Matematika
Sebuah segitiga mempunyai tinggi 20 cm dan alas 8 cm. Luas segitiga tersebut adalah ... cm2
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Segitiga
Kelas IV
Kurikulum 2013
K13
Matematika
Ulasan Buku The Hobbit Karya J.R.R. Tolkien
Bilbo terlibat ke dalam sebuah petualangan yang menegangkan. Ada tiga belas kurcaci yang mendatangi rumah Bilbo karena mengiranya seorang pencuri berpengalaman. Bilbo pun terpaksa bergabung ke dalam petualangan para kurcaci. Mereka pergi untuk mencari Smaug, seekor naga jahat yang telah merampas harta karun milik kurcaci.
Di tengah perjalanan, mereka dihadang oleh para goblin. Bilbo dan para kurcaci pun lari dari kejaran goblin. Namun Bilbo malah tersesat di gua Gollum. Di sana, ia menemukan cincin ajaib yang bisa membuat tubuhnya tidak terlihat.

Sampul buku The Hobbit karya J.R.R Tolkien, diterbitkan oleh Gramedia
Buku ini berisi cerita tentang seorang hobbit yang melakukan petualangan bersama 13 kurcaci. Hobbit adalah sejenis manusia yang mempunyai tubuh kerdil dan tinggal di sebuah lubang di tanah. Buku ini menawarkan jenis cerita fantasi, kejadian yang tidak ditemukan dalam dunia nyata. Cerita fantasi dalam cerita ini, di antaranya, makhluk goblin, naga, penyihir, pohon yang bisa berbicara, dan sebagainya.
Kelebihan dalam buku ini adalah tokoh-tokohnya yang unik. Di dalam buku ini banyak terdapat tokoh fabel (hewan) dan tumbuhan yang bisa berbicara. Kelebihan lain dalam buku ini adalah pada gaya bahasanya. Buku ini menggunakan gaya bahasa kiasan.
Buku ini sangat menginspirasi anak-anak karena mengajarkan arti persahabatan melalui cerita Bilbo dan 13 kurcaci dalam menyelesaikan misi. Selain itu, buku ini juga memberi pelajaran untuk jangan menjadi orang yang tamak seperti Smaug.
Berdasarkan ulasan di atas, Bilbo tersesat ke dalam gua dan menemukan cincin ajaib. Keajaiban cincin tersebut adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra
Bilangan kelipatan 6 yang kurang dari 20 adalah . . .
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Kelipatan Bilangan
Kelas IV
Kurikulum 2013
K13
Matematika
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Vocabulary: Jobs
Kelas IV
Kurikulum 2013
K13
Sebuah taman mempunyai panjang sisi 14 m. Luas taman tersebut adalah ... m2
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Persegi
Kelas IV
Kurikulum 2013
K13
Matematika
Faktorisasi prima dari 48 adalah …
Matematika
Level 4
Bilangan
FPB dan KPK
Faktor dan Faktorisasi Prima
Kelas IV
Kurikulum 2013
K13
Matematika
Cermati teks berikut!
Jaka Tarub

Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Cerita Rakyat
Video
Kelas IV
Kurikulum 2013
K13
Bahasa Indonesia
-4" + 4o - 4' = ...
Matematika
Level 4
Geometri
Garis dan Sudut
Sudut
Kelas IV
Kurikulum 2013
K13
Matematika
Perhatikan diagram berikut!
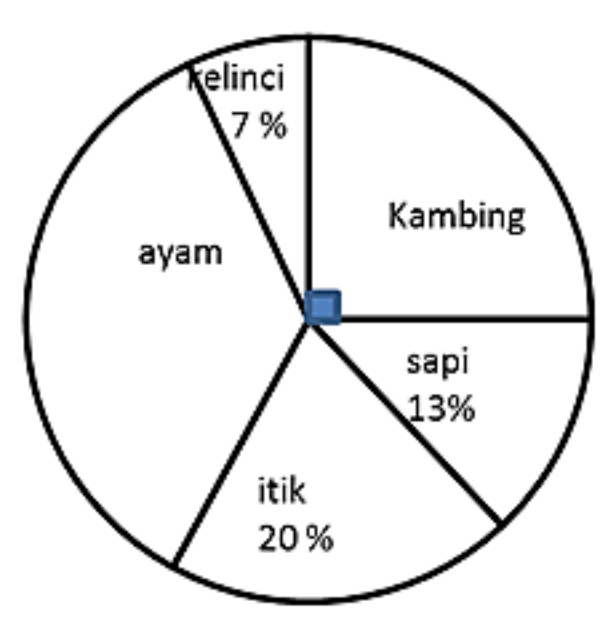
Pernyataan yang benar berdasarkan diagram di atas adalah ...
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Kelas IV
Kurikulum 2013
K13
Matematika
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pecahan yang senilai dengan pecahan di atas adalah ...
Sebuah segitiga mempunyai tinggi 20 cm dan alas 8 cm. Luas segitiga tersebut adalah ... cm2
Ulasan Buku The Hobbit Karya J.R.R. Tolkien
Bilbo terlibat ke dalam sebuah petualangan yang menegangkan. Ada tiga belas kurcaci yang mendatangi rumah Bilbo karena mengiranya seorang pencuri berpengalaman. Bilbo pun terpaksa bergabung ke dalam petualangan para kurcaci. Mereka pergi untuk mencari Smaug, seekor naga jahat yang telah merampas harta karun milik kurcaci.
Di tengah perjalanan, mereka dihadang oleh para goblin. Bilbo dan para kurcaci pun lari dari kejaran goblin. Namun Bilbo malah tersesat di gua Gollum. Di sana, ia menemukan cincin ajaib yang bisa membuat tubuhnya tidak terlihat.
Sampul buku The Hobbit karya J.R.R Tolkien, diterbitkan oleh Gramedia
Buku ini berisi cerita tentang seorang hobbit yang melakukan petualangan bersama 13 kurcaci. Hobbit adalah sejenis manusia yang mempunyai tubuh kerdil dan tinggal di sebuah lubang di tanah. Buku ini menawarkan jenis cerita fantasi, kejadian yang tidak ditemukan dalam dunia nyata. Cerita fantasi dalam cerita ini, di antaranya, makhluk goblin, naga, penyihir, pohon yang bisa berbicara, dan sebagainya.
Kelebihan dalam buku ini adalah tokoh-tokohnya yang unik. Di dalam buku ini banyak terdapat tokoh fabel (hewan) dan tumbuhan yang bisa berbicara. Kelebihan lain dalam buku ini adalah pada gaya bahasanya. Buku ini menggunakan gaya bahasa kiasan.
Buku ini sangat menginspirasi anak-anak karena mengajarkan arti persahabatan melalui cerita Bilbo dan 13 kurcaci dalam menyelesaikan misi. Selain itu, buku ini juga memberi pelajaran untuk jangan menjadi orang yang tamak seperti Smaug.
Berdasarkan ulasan di atas, Bilbo tersesat ke dalam gua dan menemukan cincin ajaib. Keajaiban cincin tersebut adalah ....
Bilangan kelipatan 6 yang kurang dari 20 adalah . . .
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Sebuah taman mempunyai panjang sisi 14 m. Luas taman tersebut adalah ... m2
Faktorisasi prima dari 48 adalah …
Cermati teks berikut!
Jaka Tarub
Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
-4" + 4o - 4' = ...
Perhatikan diagram berikut!
Pernyataan yang benar berdasarkan diagram di atas adalah ...