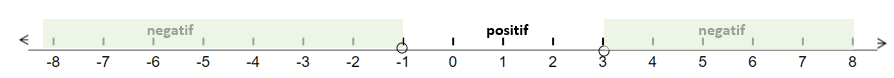Bank Soal Matematika SMA Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dua buah uang logam dilempar secara bersama-sama sebanyak 200 kali. Berapa frekuensi harapan muncul angka?
Matematika
Level 8
Statistika
Peluang
Frekuensi Harapan
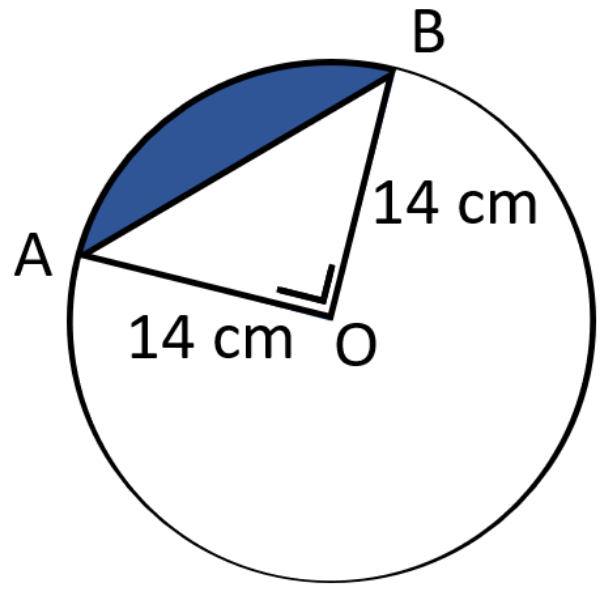
Luas daerah yang diwarnai adalah ... cm2 ( Gunakan = )
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Perhatikan gambar berikut!
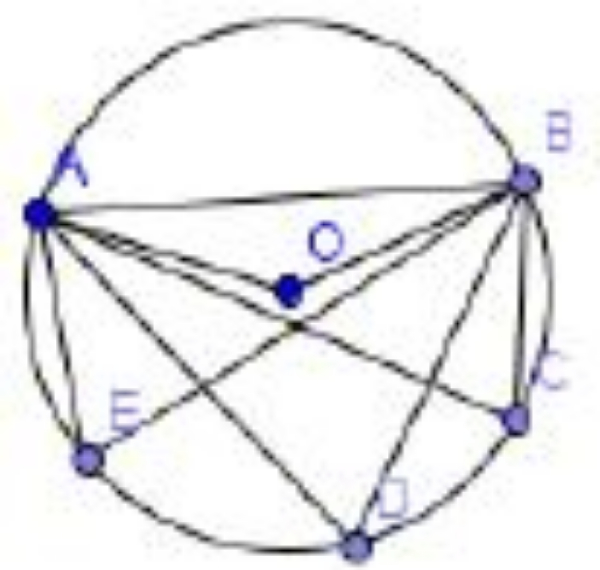
Titik O adalah titik pusat lingkaran. Diketahui sudut ACB + sudut ADB + sudut AEB = 234o. Tentukan besar sudut ACB!
Matematika
Level 8
Geometri
Lingkaran
Pada gambar koordinat cartesius di bawah ini, titik (3, 8) dan (-2, 2) ditunjukkan oleh huruf?

Matematika
Level 8
Geometri
Koordinat Kartesius
Bacalah penggalan paragraf berikut!
Susan L. Hymen, pediatris khusus penanganan tumbuh kembang anak dari Rochester University mengatakan bahwa semakin dini seorang anak terdiagnosa keterlambatan tumbuh kembang, maka kian cepat dapat teratasi masalahnya, sehingga dapat mengantisipasi kondisi tertentu.
(Sumber: difabel.tempo.co)
Kalimat tidak langsung tersebut diubah menjadi kalimat langsung menjadi ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Struktur dan Kebahasaan Teks Berita
Andy — study — hard — Kate
Which comparative sentence is correct based on the clues above?
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Diketahui dengan koordinat masing-masing titik sudutnya , , dan . Koordinat titik berat adalah ....
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik dan Bangun Datar
Cermati puisi berikut!
Aku
Kalau sampai waktuku
‘Ku mau tak seorang ‘kan merayu
Tidak juga kau
Tak perlu sedu sedan itu
Aku ini binatang jalang
Dari kumpulan yang terbuang
Biar peluru menembus kulitku
Aku tetap meradang menerjang
Luka dan bisa kubawa berlari
Berlari
Hingga hilang pedih peri
Dan aku akan lebih tidak peduli
Aku mau hidup seribu tahun lagi!
(Karya: Chairil Anwar)
Citraan yang terdapat pada larik yang dicetak miring tersebut adalah citraan ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Kedai Minuman Rina
Rina akan membuka kedai minuman kekinian minggu depan. Ia membuat poster untuk mempromosikan kedai tersebut. Perhatikan poster kedai minuman milik Rina di bawah ini!

(Sumber Gambar: foodyas.com)
Di mana kamu bisa mendapatkan informasi lebih lanjut tentang kedai minuman milik Rina?
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
When we want to ask someone's willingness to do something, we say ....
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dua buah uang logam dilempar secara bersama-sama sebanyak 200 kali. Berapa frekuensi harapan muncul angka?
Luas daerah yang diwarnai adalah ... cm2 ( Gunakan = )
Perhatikan gambar berikut!
Titik O adalah titik pusat lingkaran. Diketahui sudut ACB + sudut ADB + sudut AEB = 234o. Tentukan besar sudut ACB!
Pada gambar koordinat cartesius di bawah ini, titik (3, 8) dan (-2, 2) ditunjukkan oleh huruf?
Bacalah penggalan paragraf berikut!
Susan L. Hymen, pediatris khusus penanganan tumbuh kembang anak dari Rochester University mengatakan bahwa semakin dini seorang anak terdiagnosa keterlambatan tumbuh kembang, maka kian cepat dapat teratasi masalahnya, sehingga dapat mengantisipasi kondisi tertentu.
(Sumber: difabel.tempo.co)
Kalimat tidak langsung tersebut diubah menjadi kalimat langsung menjadi ....
Andy — study — hard — Kate
Which comparative sentence is correct based on the clues above?
Diketahui dengan koordinat masing-masing titik sudutnya , , dan . Koordinat titik berat adalah ....
Cermati puisi berikut!
Aku
Kalau sampai waktuku
‘Ku mau tak seorang ‘kan merayu
Tidak juga kau
Tak perlu sedu sedan itu
Aku ini binatang jalang
Dari kumpulan yang terbuang
Biar peluru menembus kulitku
Aku tetap meradang menerjang
Luka dan bisa kubawa berlari
Berlari
Hingga hilang pedih peri
Dan aku akan lebih tidak peduli
Aku mau hidup seribu tahun lagi!
(Karya: Chairil Anwar)
Citraan yang terdapat pada larik yang dicetak miring tersebut adalah citraan ....
Kedai Minuman Rina
Rina akan membuka kedai minuman kekinian minggu depan. Ia membuat poster untuk mempromosikan kedai tersebut. Perhatikan poster kedai minuman milik Rina di bawah ini!
(Sumber Gambar: foodyas.com)
Di mana kamu bisa mendapatkan informasi lebih lanjut tentang kedai minuman milik Rina?
When we want to ask someone's willingness to do something, we say ....