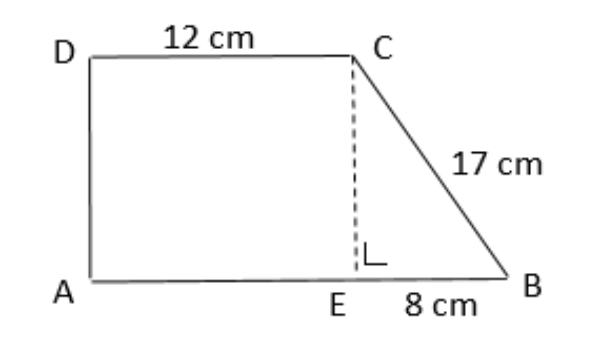
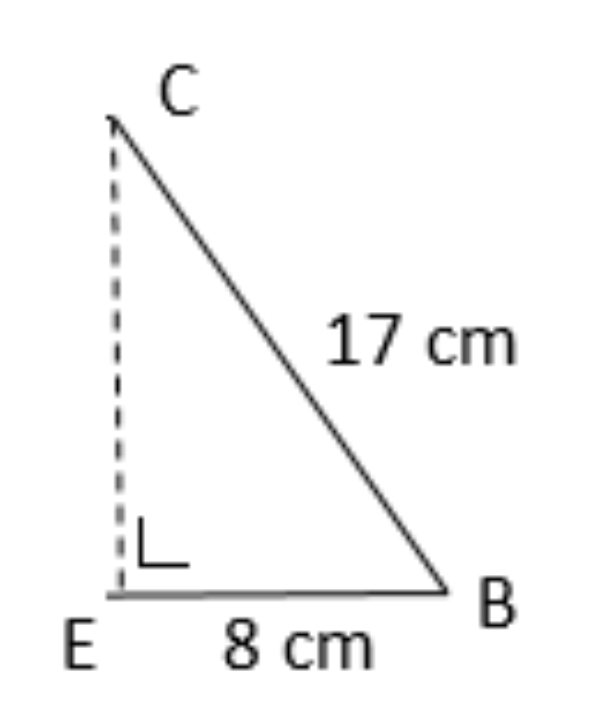
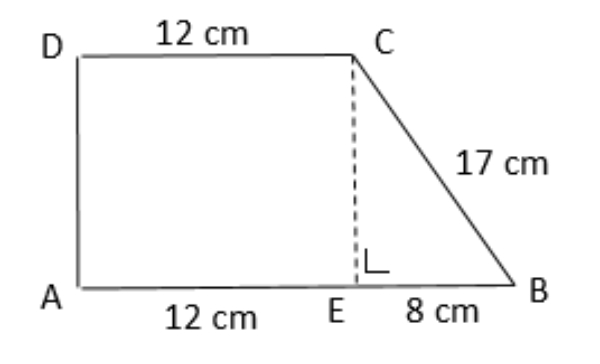
Bank Soal Matematika SMP Penerapan Teorema Pythagoras
Soal
Soal Cerita LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
Choose the correct answer.

Source: canva.com
Marlin has just won the national debate competition. Adele wants to send her a congratulation card.
The appropriate words to complete the card are ....
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting
Dari sekian banyak aturan keselamatan kerja di laboratorium, salah satunya adalah siswa tidak diperbolehkan membawa makanan atau minuman ke dalam laboratorium. Apa alasan yang tepat terkait aturan tersebut?
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
Selang ( ) dillukiskan oleh garis bilangan ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel
Yang dimaksud dengan tuyang adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Ilmu yang mempelajari hubungan timbal balik antara makhluk hidup dan lingkungannya di dalam suatu ekosistem disebut dengan istilah ....
Biologi
Level 10
Biologi
Ekologi
Ekologi dan Komponen Ekosistem
Cara pencegahan infeksi virus adalah melalui ....
Biologi
Level 10
Biologi
Virus
Pencegahan dan Pengobatan Infeksi Virus
Andi melakukan suatu percobaan di laboratorium dengan menggunakan suatu cairan tidak berwarna. Saat menuangkan cairan ke dalam gelas kaca, tanpa disengaja beberapa tetes cairan tersebut jatuh ke kulit tangan Andi. Tidak berapa lama, terlihat bahwa telah terjadi kerusakan pada kulit Andi.
Berdasarkan cerita di atas, sifat bahan kimia yang digunakan dalam percobaan tersebut adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Daerah penyelesaian dari sistem pertidaksamaan linear-kuadrat dua variabel
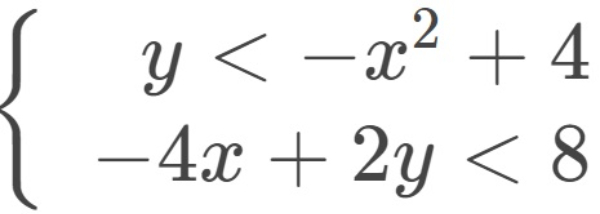
adalah ....
Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Sistem Pertidaksamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Choose the correct answer.
Source: canva.com
Marlin has just won the national debate competition. Adele wants to send her a congratulation card.
The appropriate words to complete the card are ....
Dari sekian banyak aturan keselamatan kerja di laboratorium, salah satunya adalah siswa tidak diperbolehkan membawa makanan atau minuman ke dalam laboratorium. Apa alasan yang tepat terkait aturan tersebut?
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Selang ( ) dillukiskan oleh garis bilangan ....
Yang dimaksud dengan tuyang adalah ….
Ilmu yang mempelajari hubungan timbal balik antara makhluk hidup dan lingkungannya di dalam suatu ekosistem disebut dengan istilah ....
Cara pencegahan infeksi virus adalah melalui ....
Andi melakukan suatu percobaan di laboratorium dengan menggunakan suatu cairan tidak berwarna. Saat menuangkan cairan ke dalam gelas kaca, tanpa disengaja beberapa tetes cairan tersebut jatuh ke kulit tangan Andi. Tidak berapa lama, terlihat bahwa telah terjadi kerusakan pada kulit Andi.
Berdasarkan cerita di atas, sifat bahan kimia yang digunakan dalam percobaan tersebut adalah ....
Daerah penyelesaian dari sistem pertidaksamaan linear-kuadrat dua variabel
adalah ....