Bank Soal Matematika SMA Aplikasi Integral
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Hasil dari
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Pay attention to the following picture.

Which vehicle travels in this place?
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Vocabulary: Places for Holidays and Vehicles
Alexander Graham Bell tidak ditetapkan menjadi penemu telepon karena diduga mencuri desain telepon yang sudah dibuat Antonio Meucci.
Kata tanya yang sesuai untuk informasi tersebut adalah ….
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Perhatikan gambar berikut!
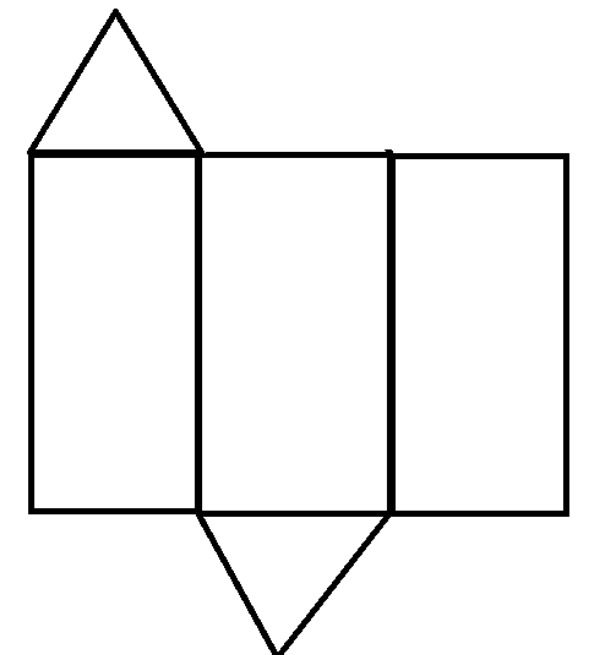
Gambar di samping merupakan jaring-jaring bangun ruang …
Matematika
Level 6
Geometri
Bangun Ruang
Sifat dan Jaring-Jaring Bangun Ruang
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Hasil
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Bagian yang harus ada dalam laporan hasil pengamatan atau kunjungan ….
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menulis Teks Laporan
Suhu udara di sebuah ruang adalah 0C. Setiap jam mengalami kenaikan suhu sebesar 20C. Suhu ruangan tersebut setelah 3 jam sebesar ... 0C
Berikut ini yang termasuk kalimat efektif adalah …
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menggali Isi
Perhatikan tabel berikut!
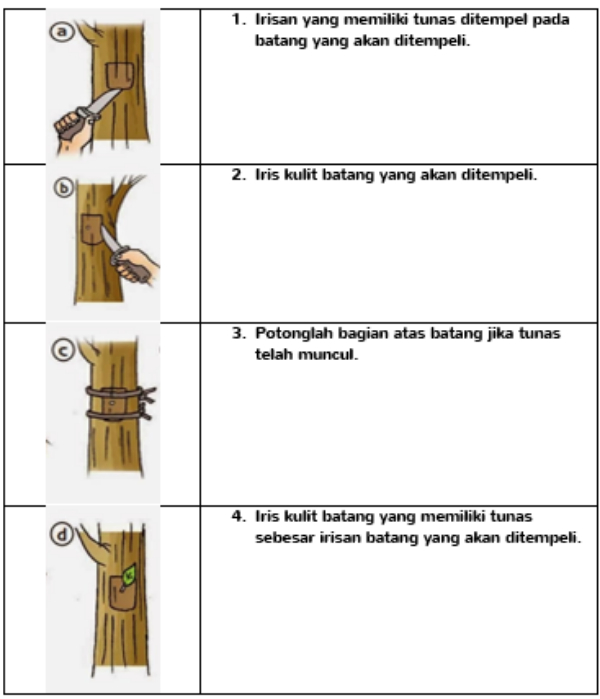
Gambar di atas menunjukkan cara perkembangbiakan tumbuhan secara okulasi. Pasangan gambar dengan keterangannya yang tepat yaitu ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Perkembangbiakan Tumbuhan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Hasil dari
Pay attention to the following picture.

Which vehicle travels in this place?
Alexander Graham Bell tidak ditetapkan menjadi penemu telepon karena diduga mencuri desain telepon yang sudah dibuat Antonio Meucci.
Kata tanya yang sesuai untuk informasi tersebut adalah ….
Perhatikan gambar berikut!
Gambar di samping merupakan jaring-jaring bangun ruang …
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Hasil
Bagian yang harus ada dalam laporan hasil pengamatan atau kunjungan ….
Suhu udara di sebuah ruang adalah 0C. Setiap jam mengalami kenaikan suhu sebesar 20C. Suhu ruangan tersebut setelah 3 jam sebesar ... 0C
Berikut ini yang termasuk kalimat efektif adalah …
Perhatikan tabel berikut!
Gambar di atas menunjukkan cara perkembangbiakan tumbuhan secara okulasi. Pasangan gambar dengan keterangannya yang tepat yaitu ....



