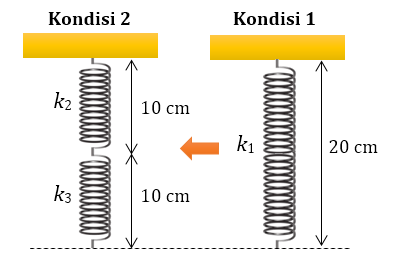
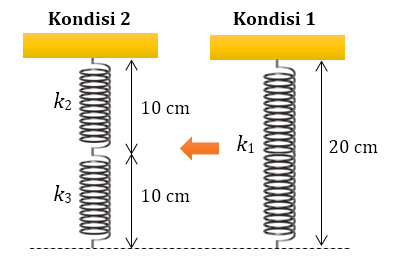
Bank Soal Fisika SMA Hukum Hooke
Soal
Soal Populer Hari Ini
31-31 = ….
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
Kelas VII
Kurikulum 2013
K13
Matematika
Nilai x pada persamaan:
2(x + 7) = x − 8 adalah ....
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Persamaan Linear Satu Variabel (PLSV)
Kelas VII
Kurikulum 2013
K13
Matematika
Perhatikan himpunan di bawah ini!
A = {t, e, h}
B = {t, h, e}
C = {x| x adalah lima bilangan cacah pertama}
D = {1, 2, 3, 4, 5}
Himpunan di atas yang sama adalah ….
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Kelas VII
Kurikulum 2013
K13
Matematika
Hubungan dua sudut yang jika dijumlahkan hasilnya adalah 180o disebut ....
Matematika
Level 7
Geometri
Garis dan Sudut
Konsep Sudut dan Garis
Kelas VII
Kurikulum 2013
K13
Matematika
Cermati contoh surat berikut ini.

Alamat pengirim surat di atas adalah ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Unsur-unsur dan Kebahasaan Surat
KD3.12
Kelas VII
Kurikulum 2013
K13
Bahasa Indonesia
Perhatikan gambar berikut!

(Sumber gambar: vectorpocket/www.freepik.com)
Teks deskripsi yang sesuai dengan ilustrasi di atas adalah ...
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Menulis Teks Deskripsi
KD4.2
Kelas VII
Kurikulum 2013
K13
Bahasa Indonesia
Hasil dari
Matematika
Level 7
Aljabar
Bentuk Aljabar
Operasi Hitung Bentuk Aljabar
Kelas VII
Kurikulum 2013
K13
Matematika
Perhatikan biografi berikut!

(Sumber gambar: akurat.co)
Salah satu penyanyi Indonesia yang pernah berduet dengan banyak penyanyi kenamaan Indonesia adalah Iwan Fals. Beliau pernah membawakan lagu berjudul Percayalah Kasih bersama Jockie Surjoprajogo dan Vina Panduwinata. Penyanyi dengan nama asli Virgiawan Lisanto ini merupakan salah satu legenda di Indonesia. Gaya musik yang dibawakannya adalah pop, rock, country, hingga folk pop. Lirik dari lagu-lagu Iwan Fals banyak menceritakan masa-masa kelam era 1970 hingga 1980-an di bidang politik. Salah satu lagunya bersama Swarmi yang berjudul Bongkar menerima penghargaan 150 lagu terbaik sepanjang masa versi Majalah Rolling Stone peringkat 1.
(Dikutip dari berbagai sumber)
Di bawah ini merupakan gaya musik yang dibawakan oleh Iwan Fals, kecuali ….
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Unsur Pembangun Buku Fiksi dan Nonfiksi
KD3.9
Kelas VII
Kurikulum 2013
K13
Bahasa Indonesia
Read the dialogue below and complete it with the best expression.
Budi: Where do you live, Irma?
Irma: ______________________________
Budi: That's quite close.
Irma: Yes.
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Self Introduction
Kelas VII
Kurikulum 2013
K13
Tabel di bawah ini memperlihatkan data jumlah penerimaan siswa per tahun ajaran di SMP Mandiri pada tahun 2019.
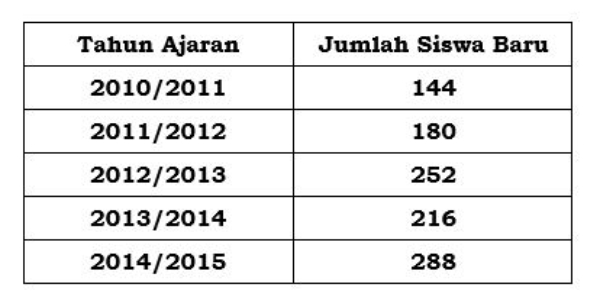
Diagram garis dari tabel tersebut adalah ....
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
Kelas VII
Kurikulum 2013
K13
Matematika
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
31-31 = ….
Nilai x pada persamaan:
2(x + 7) = x − 8 adalah ....
Perhatikan himpunan di bawah ini!
A = {t, e, h}
B = {t, h, e}
C = {x| x adalah lima bilangan cacah pertama}
D = {1, 2, 3, 4, 5}
Himpunan di atas yang sama adalah ….
Hubungan dua sudut yang jika dijumlahkan hasilnya adalah 180o disebut ....
Cermati contoh surat berikut ini.
Alamat pengirim surat di atas adalah ....
Perhatikan gambar berikut!
(Sumber gambar: vectorpocket/www.freepik.com)
Teks deskripsi yang sesuai dengan ilustrasi di atas adalah ...
Hasil dari
Perhatikan biografi berikut!
(Sumber gambar: akurat.co)
Salah satu penyanyi Indonesia yang pernah berduet dengan banyak penyanyi kenamaan Indonesia adalah Iwan Fals. Beliau pernah membawakan lagu berjudul Percayalah Kasih bersama Jockie Surjoprajogo dan Vina Panduwinata. Penyanyi dengan nama asli Virgiawan Lisanto ini merupakan salah satu legenda di Indonesia. Gaya musik yang dibawakannya adalah pop, rock, country, hingga folk pop. Lirik dari lagu-lagu Iwan Fals banyak menceritakan masa-masa kelam era 1970 hingga 1980-an di bidang politik. Salah satu lagunya bersama Swarmi yang berjudul Bongkar menerima penghargaan 150 lagu terbaik sepanjang masa versi Majalah Rolling Stone peringkat 1.
(Dikutip dari berbagai sumber)
Di bawah ini merupakan gaya musik yang dibawakan oleh Iwan Fals, kecuali ….
Read the dialogue below and complete it with the best expression.
Budi: Where do you live, Irma? Irma: ______________________________ Budi: That's quite close. Irma: Yes.
Tabel di bawah ini memperlihatkan data jumlah penerimaan siswa per tahun ajaran di SMP Mandiri pada tahun 2019.
Diagram garis dari tabel tersebut adalah ....