Bank Soal Matematika SMA Operasi Komposisi pada Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan garis bilangan dibawah ini!
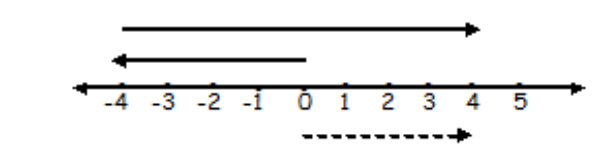
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Kelas VI
Kurikulum 2013
K13
Matematika
Pay attention to the following picture.

Which vehicle travels in this place?
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Vocabulary: Places for Holidays and Vehicles
Kelas VI
Kurikulum 2013
K13
Bacalah dengan seksama teks berikut!
Bandung Lautan Api
Pada bulan Maret 1946, dalam waktu 7 jam, sekitar 200.000 penduduk mengukir sejarah dengan membakar rumah dan harta benda mereka, meninggalkan kota menuju pegunungan di selatan. Setelah Proklamasi Kemerdekaan, 17 Agustus 1945, Indonesia belum sepenuhnya merdeka. Kemerdekaan itu harus dicapai dengan sedikit demi sedikit melalui perjuangan rakyat yang rela mengorbankan segalanya.
Ultimatum agar Tentara Republik Indonesia (TRI) meninggalkan kota dan rakyat, melahirkan politik "bumi hangus". Rakyat tidak rela bila kota Bandung dimanfaatkan oleh musuh. Mereka mengungsi ke arah selatan bersama para pejuang. Keputusan untuk membumihanguskan Bandung diambil melalui musyawarah Majelis Persatuan Perjuangan Priangan (MP3) di hadapan semua kekuatan perjuangan, pada 24 Maret 1946.
Kolonel A.H. Nasution selaku Komandan Divisi memerintahkan rakyat untuk meninggalkan Bandung. Hari itu juga, rombongan besar penduduk Bandung mengalir meninggalkan kota. Bandung dengan sengaja dibakar oleh TRI dan rakyat dengan maksud agar sekutu tidak dapat menggunakannya lagi. Banyak asap hitam mengepul membubung tinggi di udara. Semua listrik mati dan tentara Inggris mulai menyerang sehingga pertempuran sengit terjadi.
Pertempuran yang paling menegangkan terjadi di pabrik mesiu milik sekutu. TRI bermaksud untuk menghancurkan gudang tersebut. Untuk itu diutuslah pemuda bernama Muhammad Toha dan Ramdan. Kedua pemuda itu berhasil meledakkan gudang tersebut dengan granat tangan. Gudang besar itu meledak dan terbakar di dalamnya.
Sejak saat itu, kurang lebih pukul 00.00, Bandung Selatan telah kosong dari penduduk dan TRI. Namun api masih membubung membakar kota dan Bandung berubah menjadi lautan api. Strategi “bumi hangus” tersebut merupakan langkah yang tepat karena kekuatan TRI dan rakyat tidak akan sanggup melawan pihak musuh yang berkekuatan besar. Selanjutnya, TRI bersama rakyat melakukan perlawanan secara gerilya dari luar Bandung.
Istilah Bandung Lautan Api muncul dari seorang wartawan bernama Atje Bastaman, yang menyaksikan pemandangan pembakaran Bandung dari bukit Gunung Leutik di sekitar Pameungpeuk, Garut. Dari puncak, ia melihat Bandung yang memerah dari daerah Cicadas sampai dengan Cimindi.
(Sumber: materibindo.com dengan pengubahan seperlunya)
Kapan keputusan untuk membumihanguskan kota Bandung diambil?
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Prisma segitiga ABC.DEF mempunyai tinggi 20 cm. Jika segitiga tersebut mempunyai alas 18 cm dan tinggi 15 cm, maka volume prisma ABC.DEF adalah ... cm3
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Prisma
Kelas VI
Kurikulum 2013
K13
Matematika
Hasil dari , nilai adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Kelas VI
Kurikulum 2013
K13
Matematika
Suhu udara di sebuah ruang adalah 0C. Setiap jam mengalami kenaikan suhu sebesar 20C. Suhu ruangan tersebut setelah 3 jam sebesar ... 0C
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Kelas VI
Kurikulum 2013
K13
Matematika
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Limas
Kelas VI
Kurikulum 2013
K13
Matematika
Cermati penggalan laporan pengamatan berikut!

(Sumber: wired.com)
Fotosintesis adalah suatu proses biokimia untuk membentuk zat makanan atau energi berupa glukosa yang dilakukan oleh hampir semua tumbuhan. Proses fotosintesis dilakukan dengan menggunakan zat hara, karbon dioksida, dan air serta membutuhkan bantuan dari energi cahaya matahari. Fotosintesis dapat menghasilkan oksigen yang berguna bagi kelangsungan hidup makhluk hidup. Berdasarkan pengamatan, terdapat dua bagian utama dari rangkaian reaksi fotosintesis, yaitu reaksi terang atau reaksi yang memerlukan cahaya dan reaksi gelap atau reaksi yang tidak memerlukan cahaya, tetapi memerlukan karbon dioksida.
(Dikutip dari berbagai sumber)
Menurut laporan pengamatan tersebut, proses fotosintesis menggunakan bantuan ....
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menyajikan Informasi
Bahasa Indonesia
- Menentukan tema pidato
- Membuat kerangka pidato
- Mengembangkan kerangka menjadi naskah pidato
- Membuat pokok-pokok isi pidato
Urutan pembuatan naskah pidato yang tepat adalah ....
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menulis Teks Pidato
Berikut merupakan hal yang tidak tepat dalam menghadapi masa awal pubertas, yaitu ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Pubertas pada Manusia
Kelas VI
Kurikulum 2013
K13
IPA
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan garis bilangan dibawah ini!
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Pay attention to the following picture.

Which vehicle travels in this place?
Bacalah dengan seksama teks berikut!
Bandung Lautan Api
Pada bulan Maret 1946, dalam waktu 7 jam, sekitar 200.000 penduduk mengukir sejarah dengan membakar rumah dan harta benda mereka, meninggalkan kota menuju pegunungan di selatan. Setelah Proklamasi Kemerdekaan, 17 Agustus 1945, Indonesia belum sepenuhnya merdeka. Kemerdekaan itu harus dicapai dengan sedikit demi sedikit melalui perjuangan rakyat yang rela mengorbankan segalanya.
Ultimatum agar Tentara Republik Indonesia (TRI) meninggalkan kota dan rakyat, melahirkan politik "bumi hangus". Rakyat tidak rela bila kota Bandung dimanfaatkan oleh musuh. Mereka mengungsi ke arah selatan bersama para pejuang. Keputusan untuk membumihanguskan Bandung diambil melalui musyawarah Majelis Persatuan Perjuangan Priangan (MP3) di hadapan semua kekuatan perjuangan, pada 24 Maret 1946.
Kolonel A.H. Nasution selaku Komandan Divisi memerintahkan rakyat untuk meninggalkan Bandung. Hari itu juga, rombongan besar penduduk Bandung mengalir meninggalkan kota. Bandung dengan sengaja dibakar oleh TRI dan rakyat dengan maksud agar sekutu tidak dapat menggunakannya lagi. Banyak asap hitam mengepul membubung tinggi di udara. Semua listrik mati dan tentara Inggris mulai menyerang sehingga pertempuran sengit terjadi.
Pertempuran yang paling menegangkan terjadi di pabrik mesiu milik sekutu. TRI bermaksud untuk menghancurkan gudang tersebut. Untuk itu diutuslah pemuda bernama Muhammad Toha dan Ramdan. Kedua pemuda itu berhasil meledakkan gudang tersebut dengan granat tangan. Gudang besar itu meledak dan terbakar di dalamnya.
Sejak saat itu, kurang lebih pukul 00.00, Bandung Selatan telah kosong dari penduduk dan TRI. Namun api masih membubung membakar kota dan Bandung berubah menjadi lautan api. Strategi “bumi hangus” tersebut merupakan langkah yang tepat karena kekuatan TRI dan rakyat tidak akan sanggup melawan pihak musuh yang berkekuatan besar. Selanjutnya, TRI bersama rakyat melakukan perlawanan secara gerilya dari luar Bandung.
Istilah Bandung Lautan Api muncul dari seorang wartawan bernama Atje Bastaman, yang menyaksikan pemandangan pembakaran Bandung dari bukit Gunung Leutik di sekitar Pameungpeuk, Garut. Dari puncak, ia melihat Bandung yang memerah dari daerah Cicadas sampai dengan Cimindi.
(Sumber: materibindo.com dengan pengubahan seperlunya)
Kapan keputusan untuk membumihanguskan kota Bandung diambil?
Prisma segitiga ABC.DEF mempunyai tinggi 20 cm. Jika segitiga tersebut mempunyai alas 18 cm dan tinggi 15 cm, maka volume prisma ABC.DEF adalah ... cm3
Hasil dari , nilai adalah ...
Suhu udara di sebuah ruang adalah 0C. Setiap jam mengalami kenaikan suhu sebesar 20C. Suhu ruangan tersebut setelah 3 jam sebesar ... 0C
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Cermati penggalan laporan pengamatan berikut!
(Sumber: wired.com)
Fotosintesis adalah suatu proses biokimia untuk membentuk zat makanan atau energi berupa glukosa yang dilakukan oleh hampir semua tumbuhan. Proses fotosintesis dilakukan dengan menggunakan zat hara, karbon dioksida, dan air serta membutuhkan bantuan dari energi cahaya matahari. Fotosintesis dapat menghasilkan oksigen yang berguna bagi kelangsungan hidup makhluk hidup. Berdasarkan pengamatan, terdapat dua bagian utama dari rangkaian reaksi fotosintesis, yaitu reaksi terang atau reaksi yang memerlukan cahaya dan reaksi gelap atau reaksi yang tidak memerlukan cahaya, tetapi memerlukan karbon dioksida.
(Dikutip dari berbagai sumber)
Menurut laporan pengamatan tersebut, proses fotosintesis menggunakan bantuan ....
- Menentukan tema pidato
- Membuat kerangka pidato
- Mengembangkan kerangka menjadi naskah pidato
- Membuat pokok-pokok isi pidato
Urutan pembuatan naskah pidato yang tepat adalah ....
Berikut merupakan hal yang tidak tepat dalam menghadapi masa awal pubertas, yaitu ....



