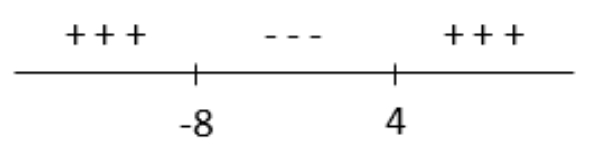
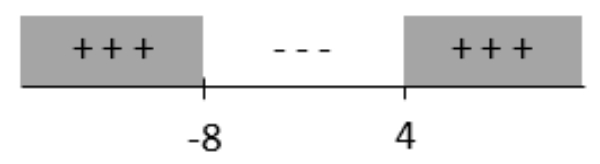
Bank Soal Matematika SMA Pertidaksamaan Kuadrat
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Hasil dari adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Campuran
Complete the sentence below.

Source: pinterest.com
Last holiday, my friends and I (1) ______. We went there by (2) ______. There, we (3) ______. It was a fun holiday!
The best word to complete point (2) is ....
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Recount Text
Perhatikan teks berikut dengan saksama.
Keanggotaan Indonesia di PBB
Perserikatan Bangsa-Bangsa (PBB) didirikan di San Fransisco, Amerika Serikat pada 24 Oktober 1945. Sidang perdana PBB diselenggarakan pada tanggal 10 Januari 1946 di Church House, London. Sidang tersebut dihadiri perwakilan dari 51 negara yang menjadi anggotanya. Saat ini, PBB mempunyai 193 negara anggota (per Oktober 2020) termasuk Indonesia.
Indonesia menjadi anggota PBB yang ke-60 pada tanggal 28 September 1950 melalui Resolusi Majelis Umum PBB. Sebelumnya, pada tanggal 14 Agustus 1947, Sutan Syahrir dan Haji Agus Salim hadir dalam sidang Dewan Keamanan PBB. Saat menjadi anggota PBB, Indonesia pernah mengirim pasukan Garuda I ke Mesir dalam misi perdamaian. Namun, pada tanggal 7 Januari 1965, Indonesia memutuskan keluar dari PBB. Pada tanggal 28 September 1966, Indonesia resmi bergabung kembali menjadi anggota PBB.
(Sumber: indonesiabaik.id dengan penyesuaian)
Indonesia pertama kali bergabung menjadi anggota PBB pada tanggal ….
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Bangun ruang yang memiliki 5 titik sudut yaitu bangun …
Matematika
Level 6
Geometri
Bangun Ruang
Sifat dan Jaring-Jaring Bangun Ruang
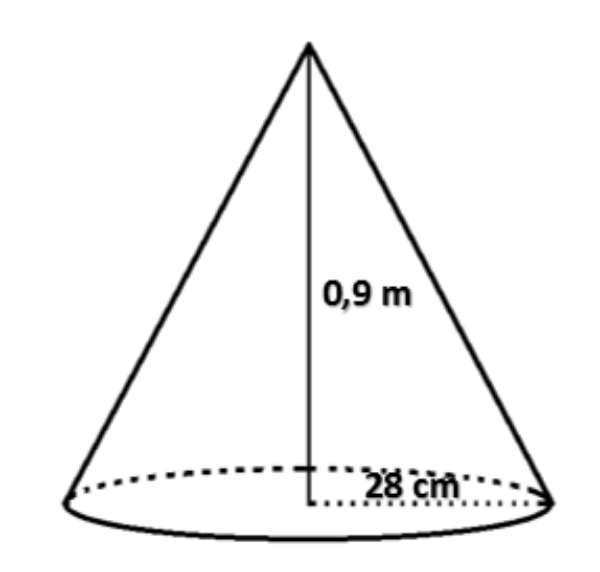
Volume kerucut di atas adalah ... liter.
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Hasil dari
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Yang perlu dicantumkan dalam laporan hasil pengamatan adalah ….
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menulis Teks Laporan
Seperempat dari sebuah bilangan sama dengan hasil kuadrat dari lima ditambah tujuh. 50% dari bilangan itu adalah ....
Saya ucapkan terima kasih karena telah memberikan kesempatan kepada saya untuk berpidato pada kesempatan kali ini. Pada kesempatan kali ini, saya akan menyampaikan pentingnya menjaga kebersihan kelas.
Penggalan teks pidato tersebut merupakan bagian ….
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menggali Isi
Menstruasi pada perempuan menandakan ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Pubertas pada Manusia
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Hasil dari adalah ...
Complete the sentence below.

Source: pinterest.com
Last holiday, my friends and I (1) ______. We went there by (2) ______. There, we (3) ______. It was a fun holiday!
The best word to complete point (2) is ....
Perhatikan teks berikut dengan saksama.
Keanggotaan Indonesia di PBB
Perserikatan Bangsa-Bangsa (PBB) didirikan di San Fransisco, Amerika Serikat pada 24 Oktober 1945. Sidang perdana PBB diselenggarakan pada tanggal 10 Januari 1946 di Church House, London. Sidang tersebut dihadiri perwakilan dari 51 negara yang menjadi anggotanya. Saat ini, PBB mempunyai 193 negara anggota (per Oktober 2020) termasuk Indonesia.
Indonesia menjadi anggota PBB yang ke-60 pada tanggal 28 September 1950 melalui Resolusi Majelis Umum PBB. Sebelumnya, pada tanggal 14 Agustus 1947, Sutan Syahrir dan Haji Agus Salim hadir dalam sidang Dewan Keamanan PBB. Saat menjadi anggota PBB, Indonesia pernah mengirim pasukan Garuda I ke Mesir dalam misi perdamaian. Namun, pada tanggal 7 Januari 1965, Indonesia memutuskan keluar dari PBB. Pada tanggal 28 September 1966, Indonesia resmi bergabung kembali menjadi anggota PBB.
(Sumber: indonesiabaik.id dengan penyesuaian)
Indonesia pertama kali bergabung menjadi anggota PBB pada tanggal ….
Bangun ruang yang memiliki 5 titik sudut yaitu bangun …
Volume kerucut di atas adalah ... liter.
Hasil dari
Yang perlu dicantumkan dalam laporan hasil pengamatan adalah ….
Seperempat dari sebuah bilangan sama dengan hasil kuadrat dari lima ditambah tujuh. 50% dari bilangan itu adalah ....
Saya ucapkan terima kasih karena telah memberikan kesempatan kepada saya untuk berpidato pada kesempatan kali ini. Pada kesempatan kali ini, saya akan menyampaikan pentingnya menjaga kebersihan kelas.
Penggalan teks pidato tersebut merupakan bagian ….
Menstruasi pada perempuan menandakan ....