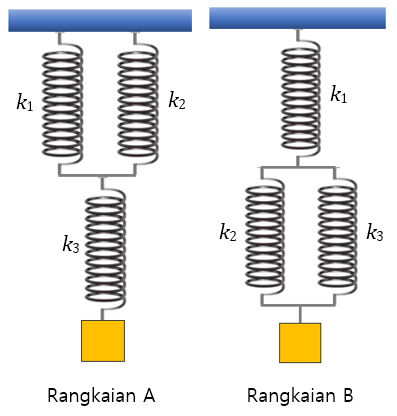
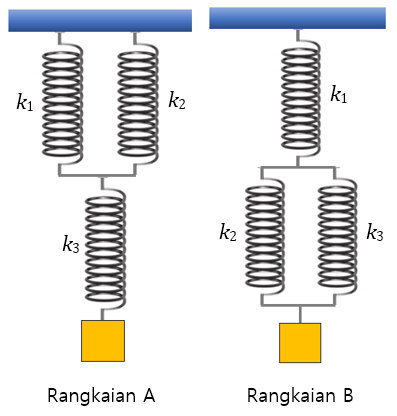
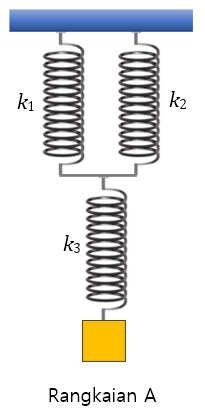
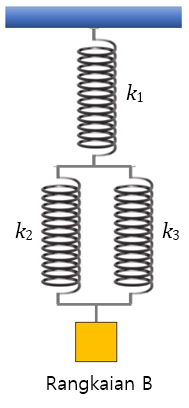
Bank Soal Fisika SMA Periode Gerak Harmonik Sederhana (GHS)
Soal
LOTS Mengaplikasikan
Soal Populer Hari Ini
Hasil dari berupa ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Kelas VI
Kurikulum 2013
K13
Matematika
Read the text and choose the right answer.

Dear diary,
I love my vacation. I arrived at the Gili Island by ship. The island was beautiful. I spent most of my time snorkeling. It was so fun!
Riana
Riana went there by ....
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Recount Text
Kelas VI
Kurikulum 2013
K13
Perhatikan penggalan paragraf dalam buku sejarah berikut!

(Sumber gambar: kebudayaan.kemdikbud.go.id)
Pada tahun 1900, di saat bangsa Indonesia mulai terbuka dalam berpikir, cara perjuangan untuk merebut kemerdekaan juga mulai menggunakan pendekatan organisasi pergerakan. Hal itu didukung juga oleh pengubahan kebijakan dari penjajah Belanda dengan mengizinkan berdirinya sekolah peribumi. Sejarah mencatat beberapa organisasi pergerakan kemerdekaan yang memengaruhi perjalanan bangsa Indonesia sampai dengan tercapainya kemerdekaan Indonesia. Adapun organisasi pergerakan tersebut antara lain adalah Budi Utomo, Sarekat Islam, Muhammadiyah, Gerakan Pemuda,Taman Siswa, Gerakan Wanita, Partai Nasional Indonesia (PNI), dan Gerakan Buruh.
Agar kalimat yang bercetak tebal menjadi kalimat efektif maka kata yang harus diubah adalah ....
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Mengembangkan Informasi
tryout
Sebuah kardus berbentuk kubus dengan panjang rusuk 84 cm. Kardus tersebut mampu memuat 392 balok satuan. Panjang balok 21 cm dan lebar 12 cm. Banyak tumpukan satuan dalam kardus adalah ....
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Kelas VI
Kurikulum 2013
K13
Matematika
(0,5 17,2) a = 30,18. Nilai a adalah …
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Campuran
Kelas VI
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!
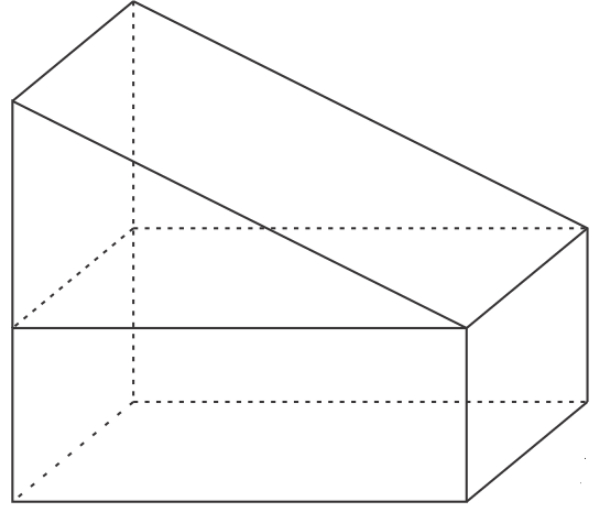
Banyak sisi pada bangun di atas adalah ....
Matematika
Level 6
Geometri
Bangun Ruang
Sifat dan Jaring-Jaring Bangun Ruang
Kelas VI
Kurikulum 2013
K13
Matematika
Berikut merupakan hal yang tidak tepat dalam menghadapi masa awal pubertas, yaitu ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Pubertas pada Manusia
Kelas VI
Kurikulum 2013
K13
IPA
Data umur anak sekolah RW 9 Desa Kemukus (dalam tahun) sebagai berikut :
15 13 14 10 13 12 15
17 12 12 13 18 14 11
Selisih umur tertinggi dan terendah adalah ... tahun
Matematika
Level 6
Statistika
Data Tunggal
Modus
Kelas VI
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!
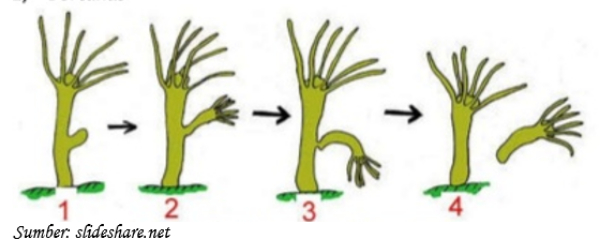
Perkembangbiakan seperti pada gambar dilakukan dengan cara ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Perkembangbiakan Hewan
Video
Kelas VI
Kurikulum 2013
K13
IPA
Ide pokok paragraf pertama teks tersebut adalah ….
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menyimpulkan Informasi
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Hasil dari berupa ...
Read the text and choose the right answer.

Dear diary,
I love my vacation. I arrived at the Gili Island by ship. The island was beautiful. I spent most of my time snorkeling. It was so fun!
Riana
Riana went there by ....
Perhatikan penggalan paragraf dalam buku sejarah berikut!
(Sumber gambar: kebudayaan.kemdikbud.go.id)
Pada tahun 1900, di saat bangsa Indonesia mulai terbuka dalam berpikir, cara perjuangan untuk merebut kemerdekaan juga mulai menggunakan pendekatan organisasi pergerakan. Hal itu didukung juga oleh pengubahan kebijakan dari penjajah Belanda dengan mengizinkan berdirinya sekolah peribumi. Sejarah mencatat beberapa organisasi pergerakan kemerdekaan yang memengaruhi perjalanan bangsa Indonesia sampai dengan tercapainya kemerdekaan Indonesia. Adapun organisasi pergerakan tersebut antara lain adalah Budi Utomo, Sarekat Islam, Muhammadiyah, Gerakan Pemuda,Taman Siswa, Gerakan Wanita, Partai Nasional Indonesia (PNI), dan Gerakan Buruh.
Agar kalimat yang bercetak tebal menjadi kalimat efektif maka kata yang harus diubah adalah ....
Sebuah kardus berbentuk kubus dengan panjang rusuk 84 cm. Kardus tersebut mampu memuat 392 balok satuan. Panjang balok 21 cm dan lebar 12 cm. Banyak tumpukan satuan dalam kardus adalah ....
(0,5 17,2) a = 30,18. Nilai a adalah …
Perhatikan gambar berikut!
Banyak sisi pada bangun di atas adalah ....
Berikut merupakan hal yang tidak tepat dalam menghadapi masa awal pubertas, yaitu ....
Data umur anak sekolah RW 9 Desa Kemukus (dalam tahun) sebagai berikut :
15 13 14 10 13 12 15
17 12 12 13 18 14 11
Selisih umur tertinggi dan terendah adalah ... tahun
Perhatikan gambar berikut!
Perkembangbiakan seperti pada gambar dilakukan dengan cara ....
Ide pokok paragraf pertama teks tersebut adalah ….