Bank Soal Matematika SMA Induksi Matematika pada Ketidaksamaan
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bagaimanakah cara mengerjakan soal ini?
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Mendorong, membujuk, atau memberikan pengaruh pada banyak orang agar tertarik pada barang atau jasa yang ditawarkan merupakan fungsi dari ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Identifikasi Informasi
Sebagai negara agraris, Indonesia terkenal dengan hasil perkebunannya yaitu ....
IPS
Level 5
Geografi
Karakteristik Geografi Wilayah Indonesia
Karakteristik Geografis
Read the text below. Then, fill in the blank with a correct verb to be.

Source: creazilla.com
My name is Claire. I live in Arizona. I am in fifth grade. I have a brother. His name is Peter. He is in fourth grade.
Based on the text, we know that Claire and Peter ... students.
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Self-Introduction
Sebuah bak mandi memiliki panjang 150 cm, lebar 50 cm dan tinggi 80 cm. Jika bak tersebut dapat terisi penuh dalam waktu 10 menit, maka debit air yang mengalir dari keran adalah … liter/detik.
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Debit
Perhatikan Jaring-jaring kubus berikut!

Jika sisi II menjadi alas maka yang menjadi sisi atas yaitu ..
Matematika
Level 5
Geometri
Balok dan Kubus
Sifat dan Jaring-Jaring Balok dan Kubus
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
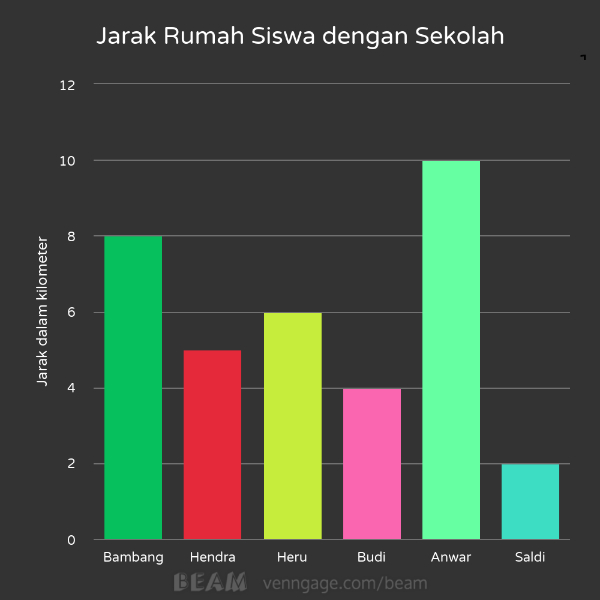
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Bacalah teks berikut!
Pedoman gizi seimbang kini telah diimplementasikan di Indonesia sebagai upaya realisasi dan rekomendasi Konferensi Pangan Sedunia di Roma tahun 1992. Pedoman tersebut menggantikan slogan "4 sehat 5 sempurna" yang telah diperkenalkan sejak tahun 1952 karena sudah tidak sesuai lagi dengan perkembangan ilmu pengetahuan dan teknologi (IPTEK) dalam bidang gizi.
Hal yang diperhatikan dalam pedoman gizi seimbang yaitu variasi makanan, pentingnya pola hidup bersih, pentingnya pola hidup aktif dan olahraga, serta memantau berat badan ideal. Dalam gambaran Tumpeng Gizi Seimbang (TGS) setiap orang dianjurkan untuk minum air putih rata-rata 8 gelas setiap harinya. Hal ini karena air merupakan bagian zat yang penting bagi kelangsungan hidup. Berikutnya disusul oleh karbohidrat yang dianjurkan untuk dikonsumsi 3-8 porsi (sesuai kebutuhan menurut usia, berat badan, dan keadaan kesehatan). Lalu sayur dan buah sebagai sumber serat, vitamin, dan mineral. Selain itu, sayuran harus lebih banyak dikonsumsi daripada buah. Kemudian, protein hewani dan nabati dikonsumsi lebih sedikit daripada sayuran dan buah. Paling puncak dilengkapi oleh minyak, gula, dan garam yang bisa digunakan seperlunya.
Judul yang tepat untuk teks eksplanasi tersebut adalah ....
Bahasa Indonesia
Level 5
Membaca
Teks Eksplanasi
Menulis Teks Eksplanasi
Perhatikan tabel berikut!

Selisih jumlah pengunjung di hari paling ramai dan paling sepi adalah sebanyak ....
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
(1) Surat pengumuman
(2) Surat perizinan
(3) Undangan ulang tahun
(4) Undangan khitanan
Yang termasuk surat undangan tidak resmi adalah nomor ….
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Identifikasi Surat Undangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bagaimanakah cara mengerjakan soal ini?
Mendorong, membujuk, atau memberikan pengaruh pada banyak orang agar tertarik pada barang atau jasa yang ditawarkan merupakan fungsi dari ....
Sebagai negara agraris, Indonesia terkenal dengan hasil perkebunannya yaitu ....
Read the text below. Then, fill in the blank with a correct verb to be.

Source: creazilla.com
My name is Claire. I live in Arizona. I am in fifth grade. I have a brother. His name is Peter. He is in fourth grade.
Based on the text, we know that Claire and Peter ... students.
Sebuah bak mandi memiliki panjang 150 cm, lebar 50 cm dan tinggi 80 cm. Jika bak tersebut dapat terisi penuh dalam waktu 10 menit, maka debit air yang mengalir dari keran adalah … liter/detik.
Perhatikan Jaring-jaring kubus berikut!
Jika sisi II menjadi alas maka yang menjadi sisi atas yaitu ..
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Bacalah teks berikut!
Pedoman gizi seimbang kini telah diimplementasikan di Indonesia sebagai upaya realisasi dan rekomendasi Konferensi Pangan Sedunia di Roma tahun 1992. Pedoman tersebut menggantikan slogan "4 sehat 5 sempurna" yang telah diperkenalkan sejak tahun 1952 karena sudah tidak sesuai lagi dengan perkembangan ilmu pengetahuan dan teknologi (IPTEK) dalam bidang gizi.
Hal yang diperhatikan dalam pedoman gizi seimbang yaitu variasi makanan, pentingnya pola hidup bersih, pentingnya pola hidup aktif dan olahraga, serta memantau berat badan ideal. Dalam gambaran Tumpeng Gizi Seimbang (TGS) setiap orang dianjurkan untuk minum air putih rata-rata 8 gelas setiap harinya. Hal ini karena air merupakan bagian zat yang penting bagi kelangsungan hidup. Berikutnya disusul oleh karbohidrat yang dianjurkan untuk dikonsumsi 3-8 porsi (sesuai kebutuhan menurut usia, berat badan, dan keadaan kesehatan). Lalu sayur dan buah sebagai sumber serat, vitamin, dan mineral. Selain itu, sayuran harus lebih banyak dikonsumsi daripada buah. Kemudian, protein hewani dan nabati dikonsumsi lebih sedikit daripada sayuran dan buah. Paling puncak dilengkapi oleh minyak, gula, dan garam yang bisa digunakan seperlunya.
Judul yang tepat untuk teks eksplanasi tersebut adalah ....
Perhatikan tabel berikut!
Selisih jumlah pengunjung di hari paling ramai dan paling sepi adalah sebanyak ....
(1) Surat pengumuman
(2) Surat perizinan
(3) Undangan ulang tahun
(4) Undangan khitanan
Yang termasuk surat undangan tidak resmi adalah nomor ….



