Bank Soal Matematika SMA Pertidaksamaan Irasional
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan tingkat organisasi kehidupan berikut!
- Jaringan
- Sel
- Populasi
- Organ
- Individu
Urutan tingkat organisasi kehidupan mulai dari yang sederhana ke kompleks adalah ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
Read the dialogue and choose the right answer.
Ananta: I just lost my girlfriend. She is my fiance now. I am so happy!
Valen: _________. I hope you have a great life together.
Ananta: That's nice of you to say so.
The suitable expressions to complete the dialogue is ...
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting

Sumber: https://www.freepik.com/
Pada saat sedang melakukan percobaan di laboratorium, Vania mengambil sampel bahan kimia yang di muka botolnya terdapat label seperti pada gambar. Tiba-tiba, tanpa sengaja bahan itu mengenai permukaan kulit tangannya. Langkah pertolongan yang tepat mengenai kecelakaan tersebut adalah ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Daerah pada ekosistem air laut yang memungkinkan terjadinya fotosintesis adalah ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tipe Ekosistem
Yang sesuai dengan sifat nilai mutlak yaitu ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Konsep Nilai Mutlak
Film Dilan: 1990 menjadi salah satu film Indonesia dengan jumlah penonton terbanyak.
Penulisan judul film yang benar adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Menulis Teks Laporan Hasil Observasi
Fosfor di alam jumlahnya sangat banyak, tetapi tidak semuanya dapat terserap pada tumbuhan. Oleh karena itu, petani pada lahan pertanian memberikan asupan fosfor dalam bentuk ....
Biologi
Level 10
Biologi
Ekologi
Produktivitas dan Daur Biogeokimia
Perhatikan jenis virus berikut!
- HIV (Human Immunodeficiency Virus)
- Bakteriofag
- Virus Influenza
- Virus corona
Dari virus di atas, virus yang menyerang sel eukariota adalah ....
Biologi
Level 10
Biologi
Virus
Cara Hidup dan Reproduksi Virus
Suatu campuran dapat dipisahkan zat-zat penyusunnya secara fisis. Contoh yang tepat untuk pemisahan secara fisis, kecuali ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Materi dan Klasifikasinya
Diketahui
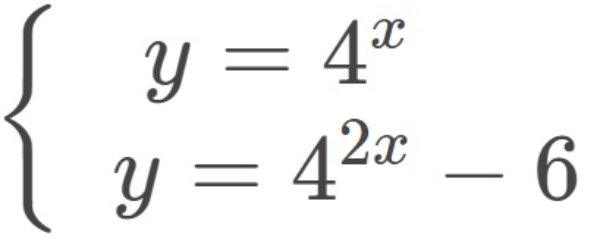
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....
Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Sistem Persamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan tingkat organisasi kehidupan berikut!
- Jaringan
- Sel
- Populasi
- Organ
- Individu
Urutan tingkat organisasi kehidupan mulai dari yang sederhana ke kompleks adalah ....
Read the dialogue and choose the right answer.
Ananta: I just lost my girlfriend. She is my fiance now. I am so happy!
Valen: _________. I hope you have a great life together.
Ananta: That's nice of you to say so.
The suitable expressions to complete the dialogue is ...
Sumber: https://www.freepik.com/
Pada saat sedang melakukan percobaan di laboratorium, Vania mengambil sampel bahan kimia yang di muka botolnya terdapat label seperti pada gambar. Tiba-tiba, tanpa sengaja bahan itu mengenai permukaan kulit tangannya. Langkah pertolongan yang tepat mengenai kecelakaan tersebut adalah ....
Daerah pada ekosistem air laut yang memungkinkan terjadinya fotosintesis adalah ....
Yang sesuai dengan sifat nilai mutlak yaitu ....
Film Dilan: 1990 menjadi salah satu film Indonesia dengan jumlah penonton terbanyak.
Penulisan judul film yang benar adalah ….
Fosfor di alam jumlahnya sangat banyak, tetapi tidak semuanya dapat terserap pada tumbuhan. Oleh karena itu, petani pada lahan pertanian memberikan asupan fosfor dalam bentuk ....
Perhatikan jenis virus berikut!
- HIV (Human Immunodeficiency Virus)
- Bakteriofag
- Virus Influenza
- Virus corona
Dari virus di atas, virus yang menyerang sel eukariota adalah ....
Suatu campuran dapat dipisahkan zat-zat penyusunnya secara fisis. Contoh yang tepat untuk pemisahan secara fisis, kecuali ....
Diketahui
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....



