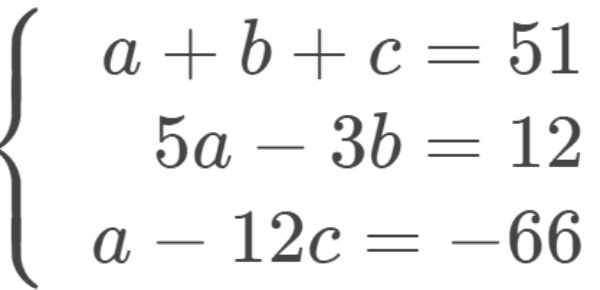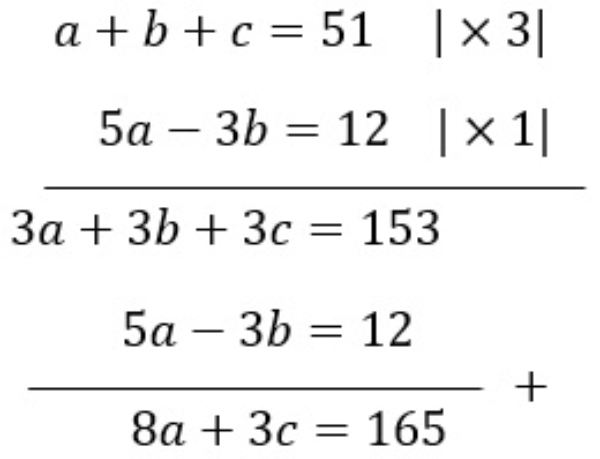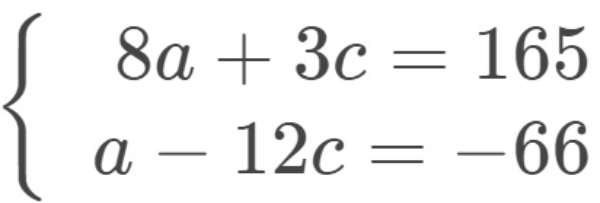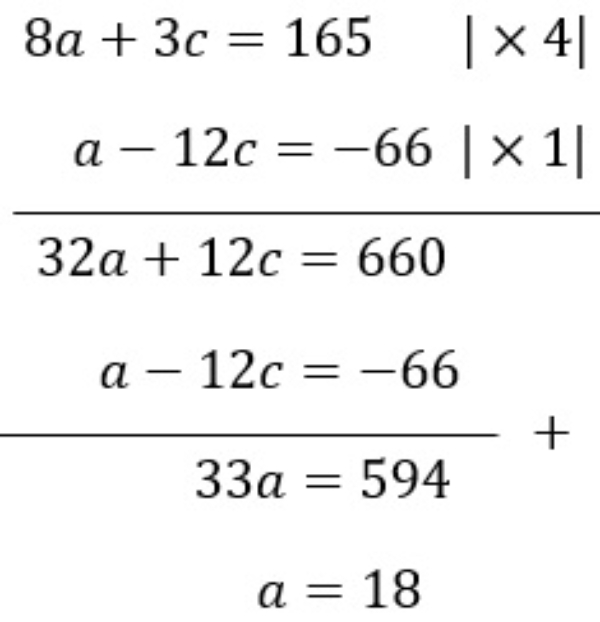Bank Soal Matematika SMA Sistem Persamaan Linear Tiga Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Adik sedang bermain kartu bilangan.

Pada kartu bilangan yang dimiliki adik, yang memiliki angka puluhan paling besar adalah kartu warna ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Kelas II
Kurikulum 2013
K13
Matematika
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Penolakan
Perhatikan bangun ruang di bawah ini.
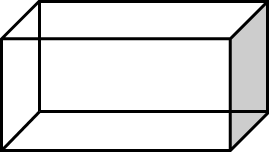
Berapa jumlah sisi yang dimiliki oleh bangun ruang tersebut?
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Rusuk, Sisi, Ruas Garis
Kelas II
Kurikulum 2013
K13
Matematika
Ibu pergi ke pasar untuk membeli beberapa bahan seperti gambar berikut.

(Sumber Gambar: dreamstime.com dan freepik.com)
Bahan yang paling murah adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Nilai Mata Uang
Kelas II
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!

(Sumber Gambar: freepik.com)
Gambar yang tepat untuk melanjutkan pola barisan di atas adalah ....
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Pola Barisan Bangun Datar
Kelas II
Kurikulum 2013
K13
Matematika

Jam seperti di atas disebut jam analog.
Jam ini biasanya mempunyai jarum pendek dan panjang.
Jarum panjang menunjuk ke angka ....
(Sumber gambar: helpingwithmath.com)
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Waktu
Kelas II
Kurikulum 2013
K13
Matematika
Didit, Mia, dan Vita adalah siswa kelas 2 SD.
Mereka memiliki uang saku yang berbeda jumlahnya.
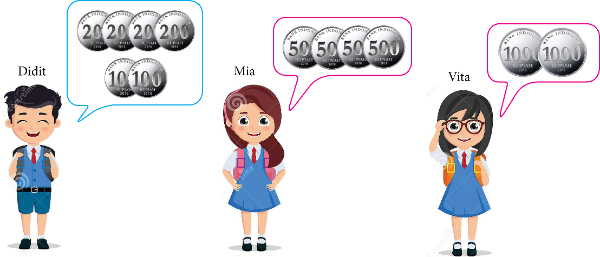
(Sumber Gambar: dreamstime.com)
Anak yang memiliki jumlah uang saku yang sama adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Kelas II
Kurikulum 2013
K13
Matematika
Arrange the jumbled letters.

Source: canva
Bahasa Inggris
Level 2
A NEW FRIEND
Shape and Colour
Kelas II
Kurikulum 2013
K13
Bahasa Inggris
Hal yang tidak perlu diperhatikan saat membaca puisi adalah ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Lafal, Intonasi, dan Ekspresi dalam Membaca Puisi
4 ratusan + 8 puluhan + 1 satuan = ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Mengenal Bilangan Cacah (500)
Kelas II
Kurikulum 2013
K13
Matematika
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Adik sedang bermain kartu bilangan.
Pada kartu bilangan yang dimiliki adik, yang memiliki angka puluhan paling besar adalah kartu warna ....
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
Perhatikan bangun ruang di bawah ini.
Berapa jumlah sisi yang dimiliki oleh bangun ruang tersebut?
Ibu pergi ke pasar untuk membeli beberapa bahan seperti gambar berikut.
(Sumber Gambar: dreamstime.com dan freepik.com)
Bahan yang paling murah adalah ....
Perhatikan gambar berikut!
(Sumber Gambar: freepik.com)
Gambar yang tepat untuk melanjutkan pola barisan di atas adalah ....
Jam seperti di atas disebut jam analog.
Jam ini biasanya mempunyai jarum pendek dan panjang.
Jarum panjang menunjuk ke angka ....
(Sumber gambar: helpingwithmath.com)
Didit, Mia, dan Vita adalah siswa kelas 2 SD.
Mereka memiliki uang saku yang berbeda jumlahnya.
(Sumber Gambar: dreamstime.com)
Anak yang memiliki jumlah uang saku yang sama adalah ....
Arrange the jumbled letters.
Source: canva
Hal yang tidak perlu diperhatikan saat membaca puisi adalah ....
4 ratusan + 8 puluhan + 1 satuan = ....