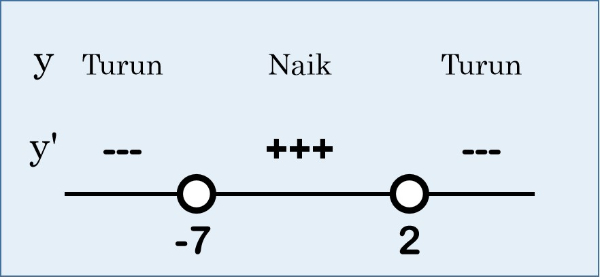
Bank Soal Matematika SMA Fungi Naik, Fungsi Turun, Nilai Stasioner
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Read the text carefully.

PANCAKES
Serve with a little caster sugar or lemon juice.
This recipe is for 2 adults and 2 kids.
Preparation time: 10 minutes
Cooking time: 15 minutes
Ingredients:
- 225 g of plain flour
- 1 egg
- 425 ml of low-fat milk
- Pinch of salt if desired
Methods:
- Sieve the flour and salt into a bowl
- Make a hoe in the center of the flour and drop in the egg with ¼ of the milk.
- Stir the egg mixture in the center of the bowl with a wooden spoon, allowing the flour to fall in gradually from the sides.
- Add the rest of the milk slowly, beating well avoid lumps.
- Pour a thin layer of the mixture onto a hot, non-stick pan.
- Use a spatula to turn the pancake over when bubbles start to appear on top.
Savory Fillings
- Chopped cooked chicken
- Smoked haddock
- Tinned salmon
- Mushrooms
- Mince cooked in curry sauce
- Bolognese sauce
Sweet Fillings
- Jam
- Stewed fruit
- Fried bananas
Source: 101 Square Meals by Safe Food
The recipe can be served for ... people.
Bahasa Inggris
Level 9
Bahasa Inggris
How to do or make things
Procedure Text
Kelas IX
Kurikulum 2013
K13
Billy has got a writing exercise. It is a review of Passive Voice.

Source: canva.com
The correct transformation for point 2 is ...
Bahasa Inggris
Level 9
Bahasa Inggris
Using passive voice to describe things
Passive Voice
Kelas IX
Kurikulum 2013
K13
Cermati Teks Berikut!
(1) Setiap makhluk hidup memerlukan makanan. (2) Makanan yang masuk ke dalam tubuh makhluk hidup akan diuraikan atau dipecah menjadi senyawa-senyawa secara sederhana, baik secara mekanik maupun secara kimiawi agar dapat diserap tubuh. (3) Tanpa makanan, makhluk hidup akan sulit mengerjakan aktivitas sehari-hari. (4) Pada umumnya bahan makanan mengandung beberapa unsur atau senyawa seperti air, karbohidrat, protein, lemak, vitamin, enzim, dan lain-lain. (5) Senyawa-senyawa tersebut sangat dibutuhkan oleh tubuh makhluk hidup.
Kalimat tidak padu pada kutipan teks tersebut ditandai dengan nomor ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
KD3.1
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Bentuk sederhana dari adalah...
Matematika
Level 9
Bilangan
Bilangan Berpangkat dan Bentuk Akar
Konsep dan Operasi Bentuk Akar
Kelas IX
Kurikulum 2013
K13
Matematika
Salah satu ciri kebahasaan yang biasanya digunakan dalam teks diskusi adalah kata rujukan. Kata rujukan adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Struktur dan Kebahasaan Teks Diskusi
KD4.9
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Enzim amilase bekerja memecah tepung menjadi maltosa, selanjutnya maltosa dihidrolisis oleh maltase menjadi glukosa.
Kata ilmiah bercetak miring mempunyai arti ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Struktur dan Kebahasaan Laporan Percobaan
KD3.2
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Persamaan teks diskusi dengan teks eksposisi adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
KD3.9
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Read the following text and answer the question.

Source: classof2020.ucsc.edu
The following statements are right about the message, except ...
Bahasa Inggris
Level 9
Bahasa Inggris
Appreciation over achievements or happiness
Expressions of Congratulations
Expressions of Congratulating
Kelas IX
Kurikulum 2013
K13
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Read the text carefully.
PANCAKES
Serve with a little caster sugar or lemon juice.
This recipe is for 2 adults and 2 kids.
Preparation time: 10 minutes
Cooking time: 15 minutes
Ingredients:
- 225 g of plain flour
- 1 egg
- 425 ml of low-fat milk
- Pinch of salt if desired
Methods:
- Sieve the flour and salt into a bowl
- Make a hoe in the center of the flour and drop in the egg with ¼ of the milk.
- Stir the egg mixture in the center of the bowl with a wooden spoon, allowing the flour to fall in gradually from the sides.
- Add the rest of the milk slowly, beating well avoid lumps.
- Pour a thin layer of the mixture onto a hot, non-stick pan.
- Use a spatula to turn the pancake over when bubbles start to appear on top.
Savory Fillings
- Chopped cooked chicken
- Smoked haddock
- Tinned salmon
- Mushrooms
- Mince cooked in curry sauce
- Bolognese sauce
Sweet Fillings
- Jam
- Stewed fruit
- Fried bananas
Source: 101 Square Meals by Safe Food
The recipe can be served for ... people.
Billy has got a writing exercise. It is a review of Passive Voice.
Source: canva.com
The correct transformation for point 2 is ...
Cermati Teks Berikut!
(1) Setiap makhluk hidup memerlukan makanan. (2) Makanan yang masuk ke dalam tubuh makhluk hidup akan diuraikan atau dipecah menjadi senyawa-senyawa secara sederhana, baik secara mekanik maupun secara kimiawi agar dapat diserap tubuh. (3) Tanpa makanan, makhluk hidup akan sulit mengerjakan aktivitas sehari-hari. (4) Pada umumnya bahan makanan mengandung beberapa unsur atau senyawa seperti air, karbohidrat, protein, lemak, vitamin, enzim, dan lain-lain. (5) Senyawa-senyawa tersebut sangat dibutuhkan oleh tubuh makhluk hidup.
Kalimat tidak padu pada kutipan teks tersebut ditandai dengan nomor ....
Bentuk sederhana dari adalah...
Salah satu ciri kebahasaan yang biasanya digunakan dalam teks diskusi adalah kata rujukan. Kata rujukan adalah ....
Enzim amilase bekerja memecah tepung menjadi maltosa, selanjutnya maltosa dihidrolisis oleh maltase menjadi glukosa.
Kata ilmiah bercetak miring mempunyai arti ....
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....
Persamaan teks diskusi dengan teks eksposisi adalah ....
Read the following text and answer the question.
Source: classof2020.ucsc.edu
The following statements are right about the message, except ...
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....