Bank Soal Matematika SMA Menentukan Nilai Limit Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bibi membeli 240 potong kue.
Bibi memberikan 120 potong kepada ibu.
Kemudian Bibi membeli lagi 75 potong.
Banyak kue yang dimiliki Bibi saat ini ada ... potong.
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Penjumlahan dan Pengurangan Bilangan Sampai 999
Bacalah teks percakapan berikut ini!
Mika: Boni, ayo, nanti sore kamu ikut bersepeda bersama aku dan Yoga.
Boni: Maaf, Mika. Aku tidak bisa ikut karena aku tidak punya sepeda.
Yoga: Kalau begitu, yuk, nanti sore kita bermain sepak bola di lapangan.
Boni: Maaf, Yoga. Aku tidak bisa ikut karena aku tidak punya sepatu sepak bola.
Mika: Baiklah. Ayo, nanti sore kita main di rumahku saja. Kebetulan aku punya mainan baru.
Yoga: Oke, Mika. Nanti sore aku akan datang ke rumahmu. Bagaimana denganmu, Boni?
Boni: Aku bisa, teman-teman. Nanti sore aku akan datang ke rumah Mika.
Ungkapan ajakan yang diucapkan Mika dalam teks percakapan di atas adalah sebagai berikut, kecuali ...
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Ajakan
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....

(Sumber: freepik.com)
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Pola Barisan Bangun Ruang
Berikut ini yang merupakan jenis uang kertas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Macam-Macam Jenis Uang
Perhatikan gambar berikut!!

(Sumber Gambar: freepik.com)
Bangun datar yang memiliki jumlah sudut paling sedikit ditunjukkan oleh nomor ....
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Sisi, Sudut, dan Titik Sudut
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.

(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Fill in the blanks.
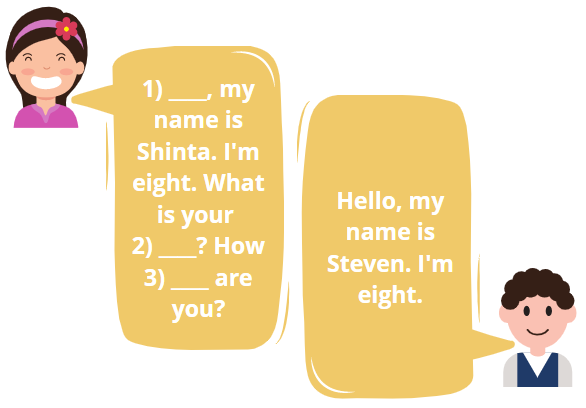
Number 3 is ______.
Bahasa Inggris
Level 2
A NEW FRIEND
Greetings and Spelling

Sumber: freepik.com
Perhatikan gambar diatas.
Jika tinggi Yudi 115 cm, maka tinggi Tyas adalah ... cm.
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Panjang
Puisi ditulis dalam bentuk ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Mencermati Isi Puisi
Adik sedang bermain kartu bilangan.

Pada kartu bilangan yang dimiliki adik, yang memiliki angka puluhan paling besar adalah kartu warna ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bibi membeli 240 potong kue.
Bibi memberikan 120 potong kepada ibu.
Kemudian Bibi membeli lagi 75 potong.
Banyak kue yang dimiliki Bibi saat ini ada ... potong.
Bacalah teks percakapan berikut ini!
Mika: Boni, ayo, nanti sore kamu ikut bersepeda bersama aku dan Yoga.
Boni: Maaf, Mika. Aku tidak bisa ikut karena aku tidak punya sepeda.
Yoga: Kalau begitu, yuk, nanti sore kita bermain sepak bola di lapangan.
Boni: Maaf, Yoga. Aku tidak bisa ikut karena aku tidak punya sepatu sepak bola.
Mika: Baiklah. Ayo, nanti sore kita main di rumahku saja. Kebetulan aku punya mainan baru.
Yoga: Oke, Mika. Nanti sore aku akan datang ke rumahmu. Bagaimana denganmu, Boni?
Boni: Aku bisa, teman-teman. Nanti sore aku akan datang ke rumah Mika.
Ungkapan ajakan yang diucapkan Mika dalam teks percakapan di atas adalah sebagai berikut, kecuali ...
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....
(Sumber: freepik.com)
Berikut ini yang merupakan jenis uang kertas adalah ....
Perhatikan gambar berikut!!
(Sumber Gambar: freepik.com)
Bangun datar yang memiliki jumlah sudut paling sedikit ditunjukkan oleh nomor ....
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.
(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Fill in the blanks.
Number 3 is ______.
Sumber: freepik.com
Perhatikan gambar diatas.
Jika tinggi Yudi 115 cm, maka tinggi Tyas adalah ... cm.
Puisi ditulis dalam bentuk ....
Adik sedang bermain kartu bilangan.
Pada kartu bilangan yang dimiliki adik, yang memiliki angka puluhan paling besar adalah kartu warna ....



