Bank Soal Matematika SMA Peluang Kejadian Majemuk
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan gambar kubus berikut!
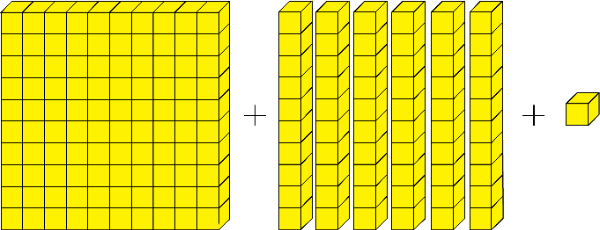
Dengan catatan:
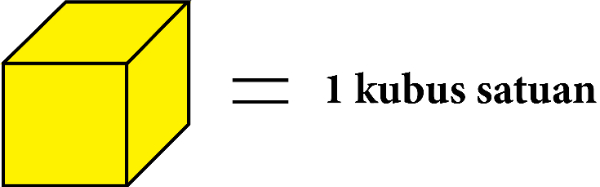
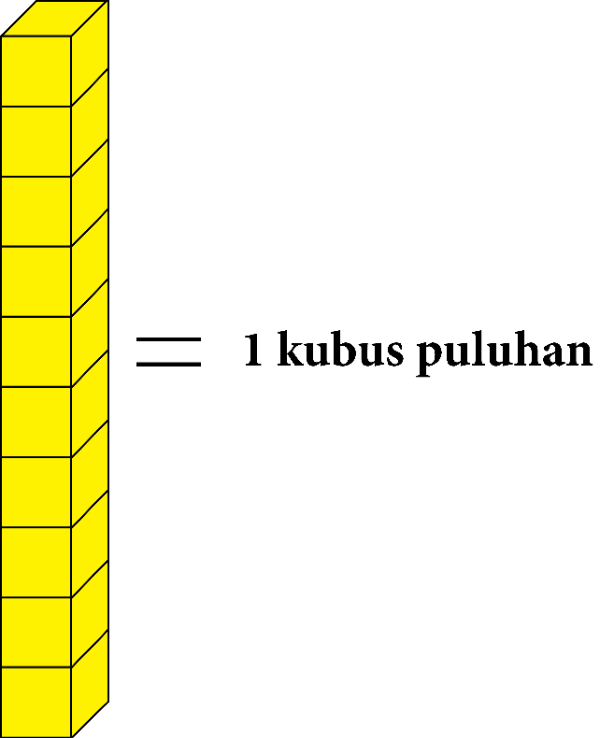
Kubus satuan yang berjumlah sepuluh digambarkan menjadi 1 kubus puluhan.
Dan kubus puluhan yang berjumlah sepuluh digambarkan menjadi kubus ratusan.
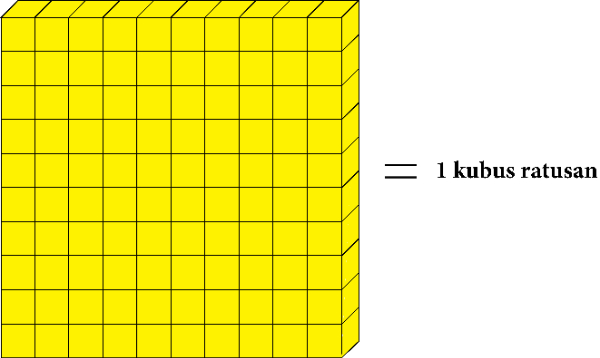
Banyaknya kubus pada gambar di atas ada ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Mengenal Bilangan Sampai 999
Rawatlah orang tuamu dengan baik!
Kalimat di atas merupakan ungkapan ....
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Perintah

Bangun ruang di atas jika diurutkan dari yang paling besar adalah ....
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Pola Barisan Bangun Ruang
Perhatikan gambar uang berikut!

(Sumber Gambar: infoperbankan.com)
Pecahan nilai uang di atas dibaca ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Nilai Mata Uang
Bangun datar yang memiliki 4 sisi sama panjang, 4 sudut siku-siku, dan 4 titik sudut adalah ....
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Ciri-Ciri Bangun Datar Sederhana
Perhatikan gambar berikut!

(Sumber Gambar: id.wikipedia.org)
Kumpulan pecahan mata uang yang nilainya setara dengan gambar di atas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Fill in the blanks.
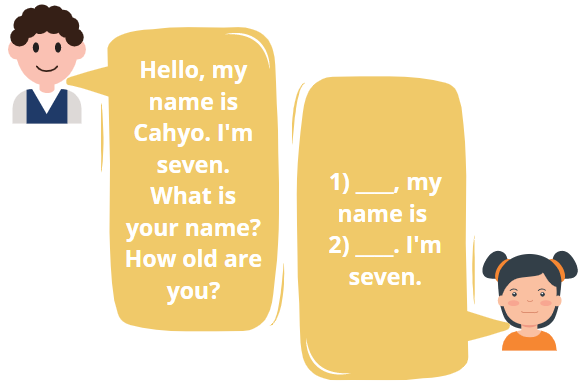
Source: canva
Number 2 is ______.
Bahasa Inggris
Level 2
A NEW FRIEND
Greetings and Spelling
Setengah jam sama dengan ... menit.
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Waktu

(Templat gambar: canva.com)
Arti kata berseri pada puisi di atas adalah ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Mencermati Isi Puisi
Terdapat dua buah bilangan.
Kedua bilangan memiliki nilai puluhan yang sama.
Tetapi bilangan pertama memiliki nilai ratusan yang lebih kecil dari bilangan kedua.
Bilangan pertama juga memiliki nilai satuan yang lebih kecil dari bilangan kedua.
Bilangan pertama dan kedua berturut-turut yang sesuai adalah ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan gambar kubus berikut!
Dengan catatan:
Kubus satuan yang berjumlah sepuluh digambarkan menjadi 1 kubus puluhan.
Dan kubus puluhan yang berjumlah sepuluh digambarkan menjadi kubus ratusan.

Banyaknya kubus pada gambar di atas ada ....
Rawatlah orang tuamu dengan baik!
Kalimat di atas merupakan ungkapan ....
Bangun ruang di atas jika diurutkan dari yang paling besar adalah ....
Perhatikan gambar uang berikut!
(Sumber Gambar: infoperbankan.com)
Pecahan nilai uang di atas dibaca ....
Bangun datar yang memiliki 4 sisi sama panjang, 4 sudut siku-siku, dan 4 titik sudut adalah ....
Perhatikan gambar berikut!
(Sumber Gambar: id.wikipedia.org)
Kumpulan pecahan mata uang yang nilainya setara dengan gambar di atas adalah ....
Fill in the blanks.
Source: canva
Number 2 is ______.
Setengah jam sama dengan ... menit.
(Templat gambar: canva.com)
Arti kata berseri pada puisi di atas adalah ....
Terdapat dua buah bilangan.
Kedua bilangan memiliki nilai puluhan yang sama.
Tetapi bilangan pertama memiliki nilai ratusan yang lebih kecil dari bilangan kedua.
Bilangan pertama juga memiliki nilai satuan yang lebih kecil dari bilangan kedua.
Bilangan pertama dan kedua berturut-turut yang sesuai adalah ....



