Bank Soal Matematika SMA Peluang Suatu Kejadian
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
sama dengan ...
Pilih semua jawaban yang benar.
Matematika
Level 4
Bilangan
Pecahan
Bentuk Pecahan
Kelas IV
Kurikulum 2013
K13
Matematika
Segitiga siku-siku KLM mempunyai alas 21 cm. Jika tinggi segitiga tersebut 28 cm, maka luasnya adalah ... cm2.
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Segitiga
Video
Kelas IV
Kurikulum 2013
K13
Matematika
Ulasan: Mata di Tanah Melus oleh Okky Madasari
Ayo ikuti petualangan ajaib Mata dengan bangsa punah Melus! Begitu kira-kira ajakan seri pertama dari novel Mata ini. Mata adalah anak perempuan berusia dua belas tahun asal Jakarta. Suatu hari orang tuanya bertengkar dan ia dibawa ibunya ke Belu, NTT. Celakanya, Mata terpisah dari ibunya. Ia tersesat di kediaman suku Melus yang konon punah tapi ternyata masih hidup di tempat rahasia. Maka mulailah pertemuan Mata dengan hal-hal ajaib, seperti Bei Nai, Dewa Buaya pelindung Melus, dan Ratu Kupu-Kupu, seorang manusia dengan sayap indah. Tidak hanya itu, Mata juga berkunjung ke masa lalu, abad ke-15-17, ketika kapal-kapal negara Eropa mulai berdatangan ke tanah ini.

Sampul novel Mata di Tanah Melus oleh Okky Madasari
Tidak hanya menggugah khayalan, novel ini juga mengandung pelajaran ilmiah. Pelajaran-pelajaran ini dibungkus oleh hal-hal ajaib dalam cerita mulai dari makhluk-makhluk gaib, perjalanan ke masa lalu, hingga makanan terlezat dari bahan tanaman. Namun sebenarnya di balik keajaiban itu, terkandung ilmu geografi (lokasi Belu, NTT), sejarah (peradaban Melus di abad lampau), dan antropologi (legenda, adat istiadat masyarakat Melus). Ini karena penulis novel benar-benar menggunakan informasi yang didapatnya ketika melakukan penelitian di Belu, NTT.
(Sumber: goodreads.com)
Berdasarkan ulasan buku sastra anak di atas, alasan Mata mengunjungi Belu, NTT adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra
Banyak faktor dari bilangan 48 adalah ...
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Faktor Bilangan
Kelas IV
Kurikulum 2013
K13
Matematika
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Vocabulary: Jobs
Kelas IV
Kurikulum 2013
K13
2 kali jumlah sisi Pentagon akan sama dengan jumlah sisi dari?
Matematika
Level 4
Geometri
Bangun Datar
Segi Banyak
Kelas IV
Kurikulum 2013
K13
Matematika
Bilangan prima mempunyai ... faktor
Matematika
Level 4
Bilangan
FPB dan KPK
Faktor dan Faktorisasi Prima
Kelas IV
Kurikulum 2013
K13
Matematika
Cermati teks berikut!
Jaka Tarub

Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Cerita Rakyat
Video
Kelas IV
Kurikulum 2013
K13
Bahasa Indonesia
(i) Sudut yang 2 kali lebih besar dari komplemen suatu sudut sebesar 21o
(ii) Sudut suplemen dari suatu sudut yang perbandingannya dengan penyikunya adalah 1:1
(iii) Sudut yang besarnya kali suplemennya
(iv) Sudut pelurus dari komplemen suatu sudut sebesar 46o
Urutan besar sudut di atas dari yang terbesar adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Kelas VII
Kurikulum 2013
K13
Matematika
Berikut adalah diagram batang jumlah coklat yang dimakan oleh sebuah keluarga di sebuah pesta.
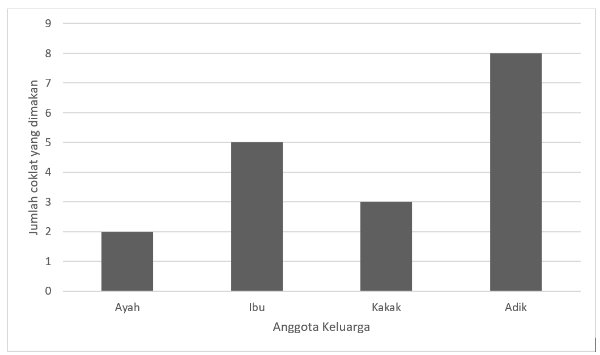
Jumlah coklat yang dimakan Ayah + Ibu ............. jumlah coklat yang dimakan Adik
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
sama dengan ...
Pilih semua jawaban yang benar.
Segitiga siku-siku KLM mempunyai alas 21 cm. Jika tinggi segitiga tersebut 28 cm, maka luasnya adalah ... cm2.
Ulasan: Mata di Tanah Melus oleh Okky Madasari
Ayo ikuti petualangan ajaib Mata dengan bangsa punah Melus! Begitu kira-kira ajakan seri pertama dari novel Mata ini. Mata adalah anak perempuan berusia dua belas tahun asal Jakarta. Suatu hari orang tuanya bertengkar dan ia dibawa ibunya ke Belu, NTT. Celakanya, Mata terpisah dari ibunya. Ia tersesat di kediaman suku Melus yang konon punah tapi ternyata masih hidup di tempat rahasia. Maka mulailah pertemuan Mata dengan hal-hal ajaib, seperti Bei Nai, Dewa Buaya pelindung Melus, dan Ratu Kupu-Kupu, seorang manusia dengan sayap indah. Tidak hanya itu, Mata juga berkunjung ke masa lalu, abad ke-15-17, ketika kapal-kapal negara Eropa mulai berdatangan ke tanah ini.
Sampul novel Mata di Tanah Melus oleh Okky Madasari
Tidak hanya menggugah khayalan, novel ini juga mengandung pelajaran ilmiah. Pelajaran-pelajaran ini dibungkus oleh hal-hal ajaib dalam cerita mulai dari makhluk-makhluk gaib, perjalanan ke masa lalu, hingga makanan terlezat dari bahan tanaman. Namun sebenarnya di balik keajaiban itu, terkandung ilmu geografi (lokasi Belu, NTT), sejarah (peradaban Melus di abad lampau), dan antropologi (legenda, adat istiadat masyarakat Melus). Ini karena penulis novel benar-benar menggunakan informasi yang didapatnya ketika melakukan penelitian di Belu, NTT.
(Sumber: goodreads.com)
Berdasarkan ulasan buku sastra anak di atas, alasan Mata mengunjungi Belu, NTT adalah ....
Banyak faktor dari bilangan 48 adalah ...
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
2 kali jumlah sisi Pentagon akan sama dengan jumlah sisi dari?
Bilangan prima mempunyai ... faktor
Cermati teks berikut!
Jaka Tarub
Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
(i) Sudut yang 2 kali lebih besar dari komplemen suatu sudut sebesar 21o
(ii) Sudut suplemen dari suatu sudut yang perbandingannya dengan penyikunya adalah 1:1
(iii) Sudut yang besarnya kali suplemennya
(iv) Sudut pelurus dari komplemen suatu sudut sebesar 46o
Urutan besar sudut di atas dari yang terbesar adalah ....
Berikut adalah diagram batang jumlah coklat yang dimakan oleh sebuah keluarga di sebuah pesta.
Jumlah coklat yang dimakan Ayah + Ibu ............. jumlah coklat yang dimakan Adik



