Bank Soal Matematika SMA Deret Geometri
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Sebuah supermarket mengadakan undian berhadiah untuk konsumennya.
Setiap konsumen dapat menukarkan kupon undian yang terkumpul untuk ditukar dengan hadiah.
Ketentuan kupon yang dapat ditukar dengan hadiah seperti gambar berikut.

(Sumber gambar: freepik.com)
Hadiah yang diperoleh untuk pengumpulan kupon yang paling sedikit menurut gambar di atas adalah ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membandingkan dan Mengurutkan Bilangan Cacah
Perhatikan nama-nama benda berikut ini!
- Es krim
- Besi
- Lilin
- Emas
Benda-benda yang susah mencair ditunjukkan oleh nomor ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menggali Informasi Konsep Perubahan Wujud Benda
Di bawah ini tabel yang menunjukkan jenis buah kesukaan siswa kelas III.
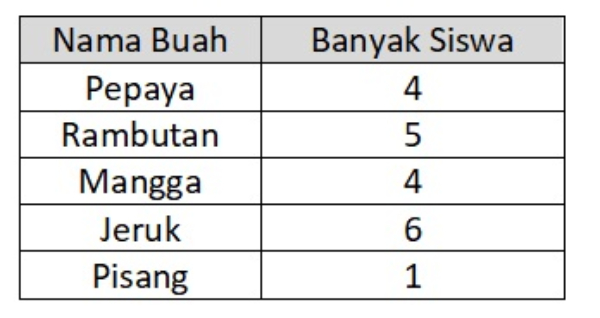
Tuliskan secara berturut-turut jenis buah yang paling sedikit dan paling banyak disukai siswa!
Matematika
Level 3
Statistika
Data
Membaca dan Menafsirkan Data
Perhatikan denah di bawah ini!
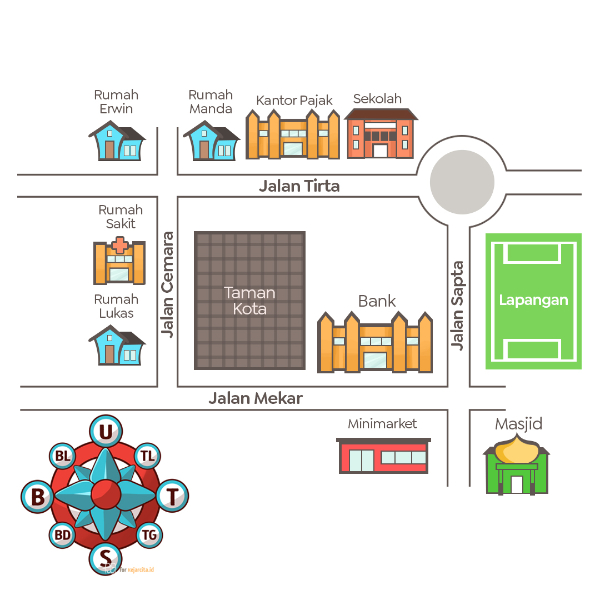
Jika Manda ingin berangkat dari rumahnya ke lapangan, maka ia harus melewati ....
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah

Pecahan yang tepat untuk mengisi titik-titik di atas adalah ....
Matematika
Level 3
Bilangan
Pecahan Sederhana
Garis Bilangan Pecahan
Anis akan mengukur panjang pensil warna miliknya dengan menggunakan penggaris.

(Sumber: freepik.com)
Panjang pensil Anis adalah ....
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Alat Ukur Panjang
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
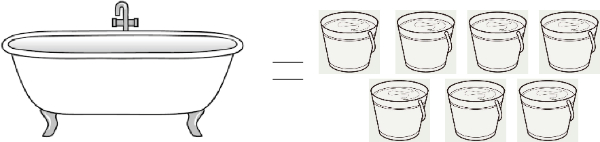
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang
Berikut yang bukan merupakan jenis sudut adalah ....
Matematika
Level 3
Geometri
Bangun Datar
Jenis dan Besar Sudut
2.300 + 1.100 = ....
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Operasi Hitung Bilangan Cacah
Tino ingin mengetahui jenis pelanggaran lalu lintas yang sering terjadi di Jalan Mawar. Narasumber yang sesuai untuk diwawancarai Tino adalah ....
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sebuah supermarket mengadakan undian berhadiah untuk konsumennya.
Setiap konsumen dapat menukarkan kupon undian yang terkumpul untuk ditukar dengan hadiah.
Ketentuan kupon yang dapat ditukar dengan hadiah seperti gambar berikut.
(Sumber gambar: freepik.com)
Hadiah yang diperoleh untuk pengumpulan kupon yang paling sedikit menurut gambar di atas adalah ....
Perhatikan nama-nama benda berikut ini!
- Es krim
- Besi
- Lilin
- Emas
Benda-benda yang susah mencair ditunjukkan oleh nomor ....
Di bawah ini tabel yang menunjukkan jenis buah kesukaan siswa kelas III.
Tuliskan secara berturut-turut jenis buah yang paling sedikit dan paling banyak disukai siswa!
Perhatikan denah di bawah ini!
Jika Manda ingin berangkat dari rumahnya ke lapangan, maka ia harus melewati ....
Pecahan yang tepat untuk mengisi titik-titik di atas adalah ....
Anis akan mengukur panjang pensil warna miliknya dengan menggunakan penggaris.
(Sumber: freepik.com)
Panjang pensil Anis adalah ....
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Berikut yang bukan merupakan jenis sudut adalah ....
2.300 + 1.100 = ....
Tino ingin mengetahui jenis pelanggaran lalu lintas yang sering terjadi di Jalan Mawar. Narasumber yang sesuai untuk diwawancarai Tino adalah ....



