Bank Soal Matematika SMA Notasi Sigma
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini

Pecahan yang tepat untuk mengisi titik-titik di atas adalah ….
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Garis Bilangan (Bilangan Cacah dan Pecahan Sederhana)
Perhatikan ilustrasi perubahan zat berikut!

Kata yang tepat untuk mengisi kotak yang kosong adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menyajikan Hasil Informasi
Berikut adalah tabel data hewan peliharaan yang dimiliki siswa kelas III.
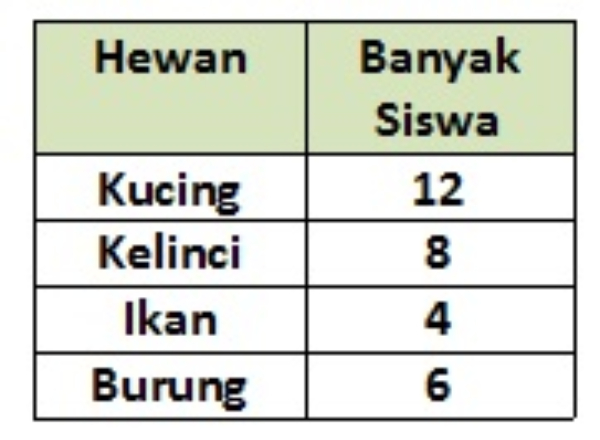
Diagram gambar yang sesuai dengan data tersebut adalah ....
Matematika
Level 3
Statistika
Data
Mengumpulkan dan Menyajikan Data
Perhatikan denah berikut!
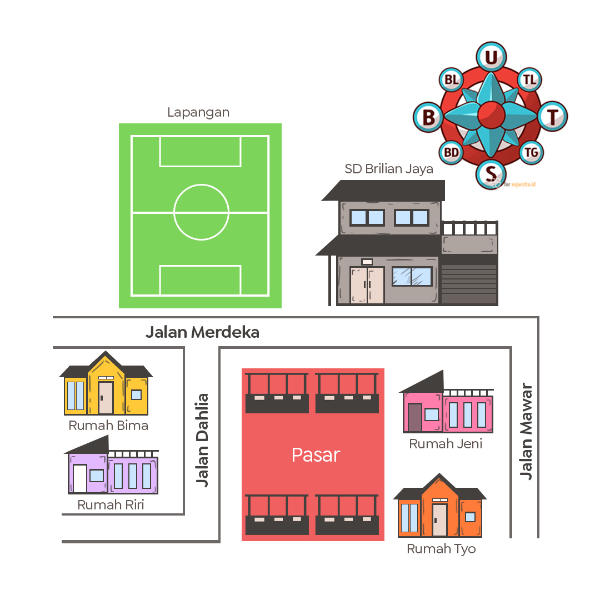
Lapangan sepak bola berada di sebelah ... rumah Jeni.
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
Anggi mempunyai dua buah apel. Setiap apel dipotong menjadi 3 bagian. Anggi memberikan dua potong kepada Susi. Dari total semua potongan apel, berapakah apel yang diterima Susi jika ditulis dalam bentuk pecahan?
Matematika
Level 3
Bilangan
Pecahan Sederhana
Menentukan Nilai Pecahan
Dimas membeli buah semangka di toko buah.
Setelah lama memilih, akhirnya Dimas memutuskan memilih salah satu buah semangka dan memberikannya kepada penjual utuk ditimbang beratnya.
Setelah ditimbang, berat buah semangka tertera pada timbangan.

(Sumber: siswapelajar.com)
Berat buah semangka tersebut adalah ....
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Alat Ukur Berat
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
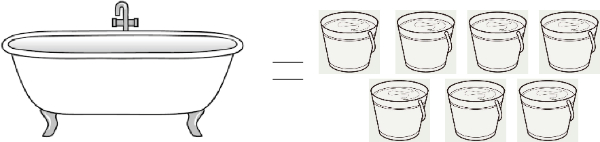
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang
Perhatikan bangun berikut!
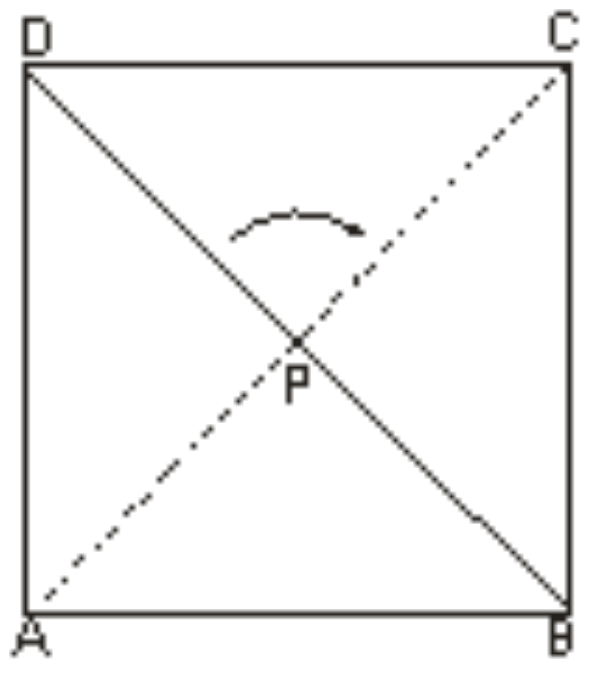
Apabila bangun ABCD diputar 180o searah jarum jam dengan titik P sebagai pusatnya, maka hasil perputaran tersebut adalah ...
Matematika
Level 3
Geometri
Bangun Datar
Simetri dan Pencerminan

Sifat distributif yang benar berada pada kolom ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Sifat-Sifat Operasi Hitung Bilangan Cacah
Cermati dialog wawancara berikut ini!
Misya: Bagaimana perasaan Kak Irfan menjadi juara satu lomba renang tingkat provinsi?
Kak Irfan: Saya merasa sangat senang dan bangga bisa mendapat juara satu.
Misya: Apa saja usaha yang Kak Irfan lakukan sehingga bisa meraih juara satu?
Kak Irfan: Latihan dengan tekun dan sungguh-sungguh.
Misya: Berapa kali Kak Irfan latihan renang dalam seminggu?
Kak Irfan: Sekitar empat sampai lima kali dalam seminggu.
Misya: Bagaimana dukungan keluarga saat Kakak mengikuti perlombaan ini?
Kak Irfan: Keluarga selalu mendukung dan mendoakan saya.
Misya: Seberapa penting dukungan dan doa dari keluarga bagi Kakak?
Kak Irfan: Sangat penting. Dukungan dan doa dari keluargalah yang membuat saya bisa meraih juara satu.
Misya: Setelah mendapat juara satu, apa yang akan Kakak lakukan dalam waktu dekat ini?
Kak Irfan: Saya masih terus berlatih renang karena sebentar lagi ada lomba renang tingkat nasional.
Narasumber dalam teks wawancara di atas adalah ....
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pecahan yang tepat untuk mengisi titik-titik di atas adalah ….
Perhatikan ilustrasi perubahan zat berikut!
Kata yang tepat untuk mengisi kotak yang kosong adalah ....
Berikut adalah tabel data hewan peliharaan yang dimiliki siswa kelas III.
Diagram gambar yang sesuai dengan data tersebut adalah ....
Perhatikan denah berikut!
Lapangan sepak bola berada di sebelah ... rumah Jeni.
Anggi mempunyai dua buah apel. Setiap apel dipotong menjadi 3 bagian. Anggi memberikan dua potong kepada Susi. Dari total semua potongan apel, berapakah apel yang diterima Susi jika ditulis dalam bentuk pecahan?
Dimas membeli buah semangka di toko buah.
Setelah lama memilih, akhirnya Dimas memutuskan memilih salah satu buah semangka dan memberikannya kepada penjual utuk ditimbang beratnya.
Setelah ditimbang, berat buah semangka tertera pada timbangan.
(Sumber: siswapelajar.com)
Berat buah semangka tersebut adalah ....
Ayah ingin berendam di bak mandi
Ayah mengisi bak mandi hingga penuh.
(Sumber Gambar: keramikdindingteras.com dan gambarmewarnai2019.blogspot.com)
Volume air dalam bak mandi yang diisi ayah adalah ....
Perhatikan bangun berikut!
Apabila bangun ABCD diputar 180o searah jarum jam dengan titik P sebagai pusatnya, maka hasil perputaran tersebut adalah ...
Sifat distributif yang benar berada pada kolom ….
Cermati dialog wawancara berikut ini!
Misya: Bagaimana perasaan Kak Irfan menjadi juara satu lomba renang tingkat provinsi?
Kak Irfan: Saya merasa sangat senang dan bangga bisa mendapat juara satu.
Misya: Apa saja usaha yang Kak Irfan lakukan sehingga bisa meraih juara satu?
Kak Irfan: Latihan dengan tekun dan sungguh-sungguh.
Misya: Berapa kali Kak Irfan latihan renang dalam seminggu?
Kak Irfan: Sekitar empat sampai lima kali dalam seminggu.
Misya: Bagaimana dukungan keluarga saat Kakak mengikuti perlombaan ini?
Kak Irfan: Keluarga selalu mendukung dan mendoakan saya.
Misya: Seberapa penting dukungan dan doa dari keluarga bagi Kakak?
Kak Irfan: Sangat penting. Dukungan dan doa dari keluargalah yang membuat saya bisa meraih juara satu.
Misya: Setelah mendapat juara satu, apa yang akan Kakak lakukan dalam waktu dekat ini?
Kak Irfan: Saya masih terus berlatih renang karena sebentar lagi ada lomba renang tingkat nasional.
Narasumber dalam teks wawancara di atas adalah ....



