Bank Soal Matematika SMA Induksi Matematika pada Barisan Bilangan
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Ayah memiliki peternakan ayam.
Ayah selalu mencatat jumlah telur yang dihasilkan setiap bulan.
Berikut adalah daftar jumlah telur yang dihasilkan selama bulan Januari - Juni.

Urutan bulan yang menghasilkan jumlah telur dari yang paling banyak ke yang paling sedikit adalah ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membandingkan dan Mengurutkan Bilangan Cacah
Perhatikan nama-nama benda berikut ini!
- Es krim
- Besi
- Lilin
- Emas
Benda-benda yang susah mencair ditunjukkan oleh nomor ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menggali Informasi Konsep Perubahan Wujud Benda
Perhatikan data hasil penjualan beberapa buah di sebuah swalayan selama hari Kamis di bawah ini.
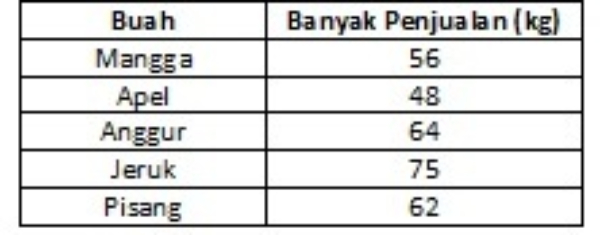 Ada berapa jenis buah yang terjual pada hari Kamis?
Ada berapa jenis buah yang terjual pada hari Kamis?
Matematika
Level 3
Statistika
Data
Mengumpulkan dan Menyajikan Data
Perhatikan denah berikut!
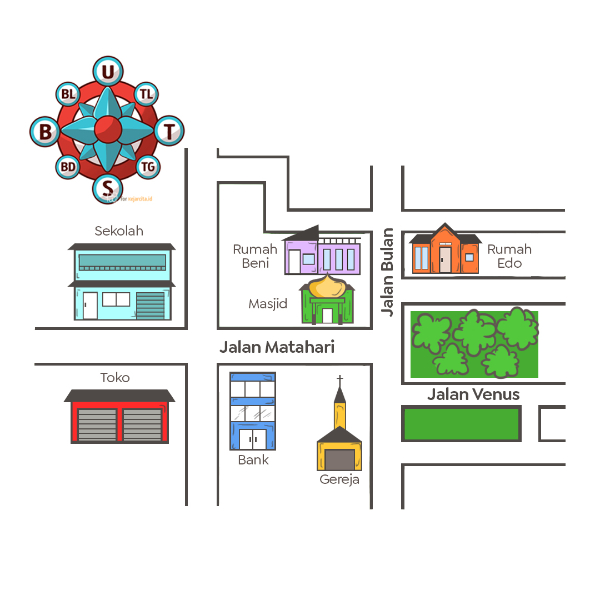
Berdasarkan denah, rumah Beni berada di ... masjid.
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
....
Matematika
Level 3
Bilangan
Pecahan Sederhana
Pengurangan Pecahan Penyebut Sama
Andi, Jordan, Meika dan Reni berolahraga untuk mengisi waktu akhir pekan. Mereka jogging dari pukul 06.32.27 hingga pukul 07.15.19. Lalu mereka bermain basket dari pukul 08.02.45 hingga pukul 09.00.11. Berapakah total waktu mereka berolahraga (jogging dan basket)?
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Hubungan Antarsatuan Waktu
Faiz mempunyai aquarium.
Air dalam aquarium habis dipindah ke dalam ember, seperti gambar berikut.

(Sumber Gambar: flaticon.com)
Arti dari gambaran di atas adalah ...
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang

Shela mengamati jendela kamarnya.
Jendela itu berbentuk persegi panjang. Panjang jendela tersebut adalah 90 cm dan lebarnya adalah 40 cm.
Luas jendela di kamar Shela adalah ....
Matematika
Level 3
Geometri
Bangun Datar
Keliling dan Luas Bangun Datar
14 16 = ....
Bilangan yang tepat untuk mengisi titik - titik di atas adalah ....
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Operasi Hitung Bilangan Cacah
Menentukan narasumber dilakukan [...] wawancara.
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Ayah memiliki peternakan ayam.
Ayah selalu mencatat jumlah telur yang dihasilkan setiap bulan.
Berikut adalah daftar jumlah telur yang dihasilkan selama bulan Januari - Juni.
Urutan bulan yang menghasilkan jumlah telur dari yang paling banyak ke yang paling sedikit adalah ....
Perhatikan nama-nama benda berikut ini!
- Es krim
- Besi
- Lilin
- Emas
Benda-benda yang susah mencair ditunjukkan oleh nomor ....
Perhatikan data hasil penjualan beberapa buah di sebuah swalayan selama hari Kamis di bawah ini.

Perhatikan denah berikut!
Berdasarkan denah, rumah Beni berada di ... masjid.
....
Andi, Jordan, Meika dan Reni berolahraga untuk mengisi waktu akhir pekan. Mereka jogging dari pukul 06.32.27 hingga pukul 07.15.19. Lalu mereka bermain basket dari pukul 08.02.45 hingga pukul 09.00.11. Berapakah total waktu mereka berolahraga (jogging dan basket)?
Faiz mempunyai aquarium.
Air dalam aquarium habis dipindah ke dalam ember, seperti gambar berikut.
(Sumber Gambar: flaticon.com)
Arti dari gambaran di atas adalah ...
Shela mengamati jendela kamarnya.
Jendela itu berbentuk persegi panjang. Panjang jendela tersebut adalah 90 cm dan lebarnya adalah 40 cm.
Luas jendela di kamar Shela adalah ....
14 16 = ....
Bilangan yang tepat untuk mengisi titik - titik di atas adalah ....
Menentukan narasumber dilakukan [...] wawancara.



