Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dua buah uang logam dilempar secara bersama-sama sebanyak 48 kali. Berapa frekuensi harapan muncul 2 gambar?
Matematika
Level 8
Statistika
Peluang
Frekuensi Harapan
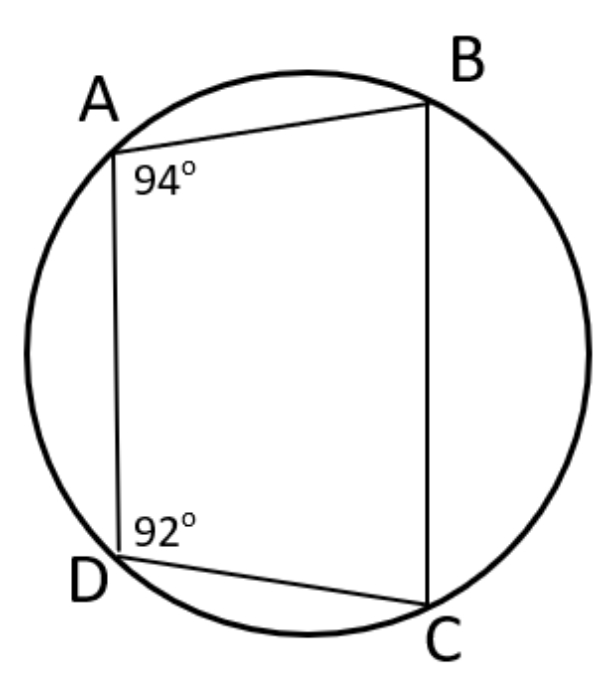
Jika dan , maka perbandingan terhadap adalah ...
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Perhatikan gambar berikut!
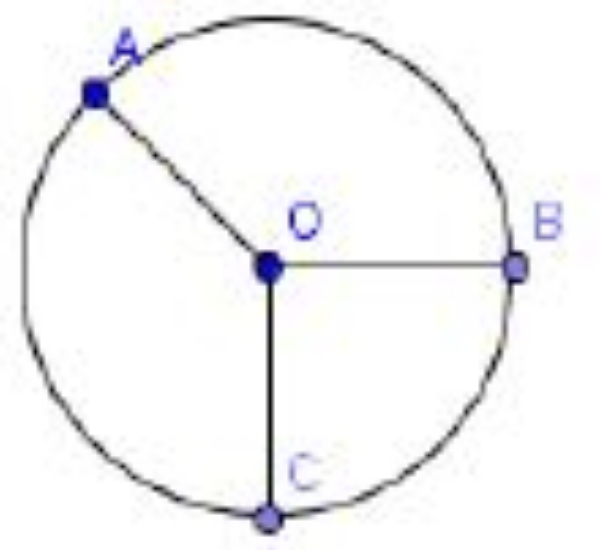
Diketahui panjagn busur AB dan busur BC berturut-turut adalah 33 cm dan 22 cm. Jika luas juring BOC adalah 154 cm2, berapakah luas juring AOB?
Matematika
Level 8
Geometri
Lingkaran
Adit, Baba, Cahyo, dan Dedi tengah duduk di sebuah bangku pada suatu lorong. Adit duduk di posisi kedua dari kanan dan bersebelahan dengan Baba. Cahyo dan Dedi masing-masing berada diposisi ujung bangku. Jika Cahyo dan Baba mengapit Adit, maka ketika Ella datang, dimanakah posisi Ella saat duduk dibangku yang sama?
Matematika
Level 8
Geometri
Koordinat Kartesius
Pengertian berita adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Unsur-unsur Berita
Read the following comments of a broadway show.

Template/source: canva.com, linetv.com
Which of the following statements is true based on the comments above?
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
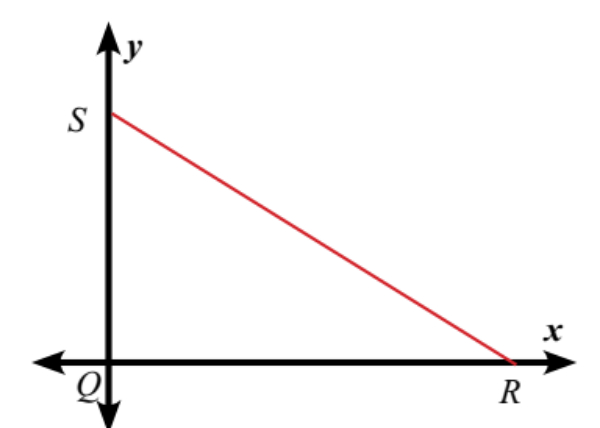
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik terhadap Titik Tertentu
Di bawah ini yang termasuk struktur batin dalam puisi adalah ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Kementerian Pendidikan dan Kebudayaan membuat sebuah slogan untuk pendidikan Indonesia. Slogan tersebut berbunyi Merdeka Belajar.
Slogan Merdeka Belajar cocok untuk pendidikan Indonesia karena ....
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Simpulan Isi Iklan, Slogan, Poster

Source: canva.com
What's the most possible answer for point 1?
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dua buah uang logam dilempar secara bersama-sama sebanyak 48 kali. Berapa frekuensi harapan muncul 2 gambar?
Jika dan , maka perbandingan terhadap adalah ...
Perhatikan gambar berikut!
Diketahui panjagn busur AB dan busur BC berturut-turut adalah 33 cm dan 22 cm. Jika luas juring BOC adalah 154 cm2, berapakah luas juring AOB?
Adit, Baba, Cahyo, dan Dedi tengah duduk di sebuah bangku pada suatu lorong. Adit duduk di posisi kedua dari kanan dan bersebelahan dengan Baba. Cahyo dan Dedi masing-masing berada diposisi ujung bangku. Jika Cahyo dan Baba mengapit Adit, maka ketika Ella datang, dimanakah posisi Ella saat duduk dibangku yang sama?
Pengertian berita adalah ....
Read the following comments of a broadway show.
Template/source: canva.com, linetv.com
Which of the following statements is true based on the comments above?
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Di bawah ini yang termasuk struktur batin dalam puisi adalah ....
Kementerian Pendidikan dan Kebudayaan membuat sebuah slogan untuk pendidikan Indonesia. Slogan tersebut berbunyi Merdeka Belajar.
Slogan Merdeka Belajar cocok untuk pendidikan Indonesia karena ....
Source: canva.com
What's the most possible answer for point 1?



