Bank Soal Matematika SMA Pertidaksamaan Linear Satu Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan garis bilangan dibawah ini!
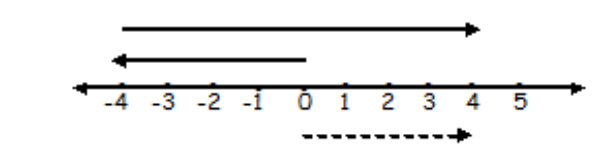
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Read the text and answer the question.

Dear diary,
…, I went to my grandma’s horse farm with my cousin. I helped grandma to feed her horses. I rode one of them too. It was exciting.
Which words are best to complete the sentence?
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Recount Text
Alexander Graham Bell tidak ditetapkan menjadi penemu telepon karena diduga mencuri desain telepon yang sudah dibuat Antonio Meucci.
Kata tanya yang sesuai untuk informasi tersebut adalah ….
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Sebuah kardus berbentuk kubus dengan panjang rusuk 84 cm. Kardus tersebut mampu memuat 392 balok satuan. Panjang balok 21 cm dan lebar 12 cm. Banyak tumpukan satuan dalam kardus adalah ....
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Suhu di dalam kulkas oC. Beberapa jam setelah aliran listrik mati, suhu naik 17oC. Sesaat setelah aliran listrik hidup kembali, suhu turun hingga 15oC. Suhu dalam kulkas sekarang adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Ide pokok paragraf pertama teks tersebut adalah ….
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menyimpulkan Informasi
Pak Min mempunyai 3 kandang ayam. Setiap kandang berisi 40 ekor ayam dan 12 ekor diantaranya ayam jantan. Pada suatu hari, semua ayam betina bertelur masing-masing 1 butir. Jika telur-telur tersebut ditempatkan dalam 14 wadah secara merata. Setiap wadah memuat telur sebanyak ... butir
(1) permohonan maaf
(2) uraian materi sesuai tema
(3) sapaan penghormatan
(4) harapan
Yang termasuk bagian penutup teks pidato adalah nomor ….
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menggali Isi
Perhatikan contoh perkembangbiakan secara vegatatif di bawah ini!
- Umbi lapis
- Umbi batang
- Cangkok
- Tunas adventif
- Merunduk
Perkembangbiakan secara vegetatif alami ditunjuk oleh nomor ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Perkembangbiakan Tumbuhan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan garis bilangan dibawah ini!
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Read the text and answer the question.

Dear diary,
…, I went to my grandma’s horse farm with my cousin. I helped grandma to feed her horses. I rode one of them too. It was exciting.
Which words are best to complete the sentence?
Alexander Graham Bell tidak ditetapkan menjadi penemu telepon karena diduga mencuri desain telepon yang sudah dibuat Antonio Meucci.
Kata tanya yang sesuai untuk informasi tersebut adalah ….
Sebuah kardus berbentuk kubus dengan panjang rusuk 84 cm. Kardus tersebut mampu memuat 392 balok satuan. Panjang balok 21 cm dan lebar 12 cm. Banyak tumpukan satuan dalam kardus adalah ....
Sebuah limas segi empat beraturan T.ABCD memiliki volume 125 cm3. Jika tinggi limas 3 kali panjang sisi alas dan tinggi sisi tegak adalah 10 cm, maka luas permukaan limas segiempat T.ABCD adalah ... cm2
Suhu di dalam kulkas oC. Beberapa jam setelah aliran listrik mati, suhu naik 17oC. Sesaat setelah aliran listrik hidup kembali, suhu turun hingga 15oC. Suhu dalam kulkas sekarang adalah ...
Ide pokok paragraf pertama teks tersebut adalah ….
Pak Min mempunyai 3 kandang ayam. Setiap kandang berisi 40 ekor ayam dan 12 ekor diantaranya ayam jantan. Pada suatu hari, semua ayam betina bertelur masing-masing 1 butir. Jika telur-telur tersebut ditempatkan dalam 14 wadah secara merata. Setiap wadah memuat telur sebanyak ... butir
(1) permohonan maaf
(2) uraian materi sesuai tema
(3) sapaan penghormatan
(4) harapan
Yang termasuk bagian penutup teks pidato adalah nomor ….
Perhatikan contoh perkembangbiakan secara vegatatif di bawah ini!
- Umbi lapis
- Umbi batang
- Cangkok
- Tunas adventif
- Merunduk
Perkembangbiakan secara vegetatif alami ditunjuk oleh nomor ....



