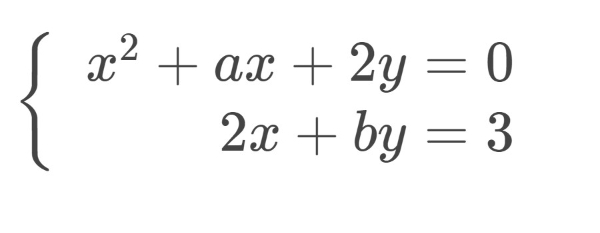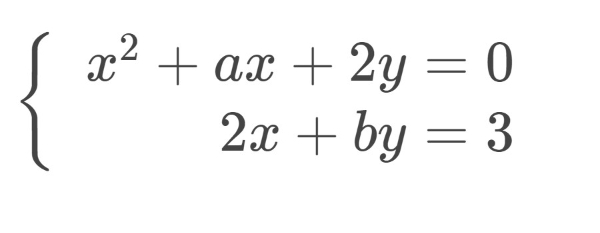Bank Soal Matematika SMA Sistem Persamaan Dua Variabel
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Hasil dari adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Campuran
Read the text and answer the question.

Dear diary,
…, I went to my grandma’s horse farm with my cousin. I helped grandma to feed her horses. I rode one of them too. It was exciting.
Which words are best to complete the sentence?
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Recount Text
Negara yang tidak termasuk kubu Sekutu adalah ….
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Prisma segitiga ABC.DEF mempunyai tinggi 20 cm. Jika segitiga tersebut mempunyai alas 18 cm dan tinggi 15 cm, maka volume prisma ABC.DEF adalah ... cm3
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang

Ibu membeli sebuah caping dari pasar. Caping tersebut berbentuk kerucut tanpa alas seperti gambar di atas. Luas permukaan caping tersebut adalah ... cm2 ( Gunakan = 3,14 )
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Hasil dari
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Bacalah laporan berikut!
Pada tanggal 12 Juni 2019 pagi hari, siswa kelas IV melakukan pengamatan di Pasar Hewan Dimoro. Banyak jenis sapi didatangkan dari peternakan di Malang, Ponorogo, hingga Probolinggo oleh para pedagang. Berbagai jenis sapi, seperti sapi limosin, sapi brahman, hingga sapi lokal ada di sana. [...]
Kalimat simpulan yang tepat untuk melengkapi teks laporan hasil pengamatan di atas agar menjadi laporan yang padu adalah ...
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menulis Teks Laporan
Seorang peternak memiliki ayam buras 150 ekor. Setiap ekor ayam menghasilkan telur rata-rata 6 butir per minggu. Telur yang rusak ada 25 butir dan tidak dapat dijual. Harga setiap butir telur Rp1.300,00. Hasil penjualan telur selama seminggu adalah ...
"Saya mengimbau siswa-siswi kelas VI untuk terus menjaga kebersihan lingkungan sekolah agar tercipta lingkungan sekolah yang asri dan nyaman."
Kutipan kalimat di atas adalah pidato bagian ....
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menulis Teks Pidato
Perubahan fisik yang terjadi pada manusia yang memasuki masa remaja disebut dengan ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Pubertas pada Manusia
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Hasil dari adalah ...
Read the text and answer the question.

Dear diary,
…, I went to my grandma’s horse farm with my cousin. I helped grandma to feed her horses. I rode one of them too. It was exciting.
Which words are best to complete the sentence?
Negara yang tidak termasuk kubu Sekutu adalah ….
Prisma segitiga ABC.DEF mempunyai tinggi 20 cm. Jika segitiga tersebut mempunyai alas 18 cm dan tinggi 15 cm, maka volume prisma ABC.DEF adalah ... cm3
Ibu membeli sebuah caping dari pasar. Caping tersebut berbentuk kerucut tanpa alas seperti gambar di atas. Luas permukaan caping tersebut adalah ... cm2 ( Gunakan = 3,14 )
Hasil dari
Bacalah laporan berikut!
Pada tanggal 12 Juni 2019 pagi hari, siswa kelas IV melakukan pengamatan di Pasar Hewan Dimoro. Banyak jenis sapi didatangkan dari peternakan di Malang, Ponorogo, hingga Probolinggo oleh para pedagang. Berbagai jenis sapi, seperti sapi limosin, sapi brahman, hingga sapi lokal ada di sana. [...]
Kalimat simpulan yang tepat untuk melengkapi teks laporan hasil pengamatan di atas agar menjadi laporan yang padu adalah ...
Seorang peternak memiliki ayam buras 150 ekor. Setiap ekor ayam menghasilkan telur rata-rata 6 butir per minggu. Telur yang rusak ada 25 butir dan tidak dapat dijual. Harga setiap butir telur Rp1.300,00. Hasil penjualan telur selama seminggu adalah ...
"Saya mengimbau siswa-siswi kelas VI untuk terus menjaga kebersihan lingkungan sekolah agar tercipta lingkungan sekolah yang asri dan nyaman."
Kutipan kalimat di atas adalah pidato bagian ....
Perubahan fisik yang terjadi pada manusia yang memasuki masa remaja disebut dengan ....