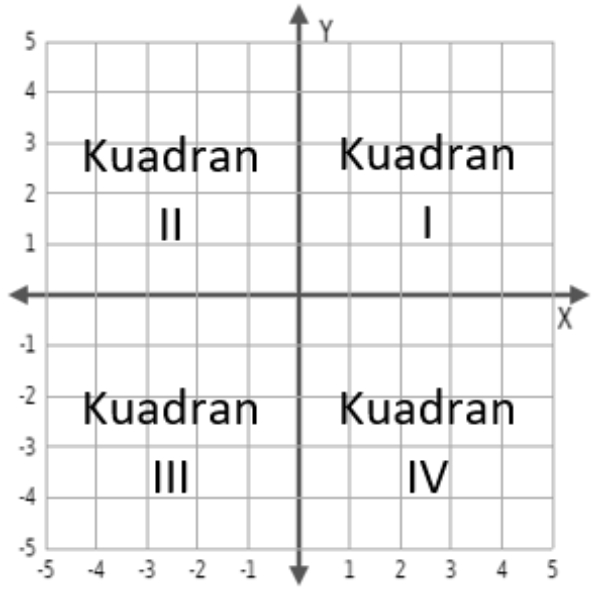
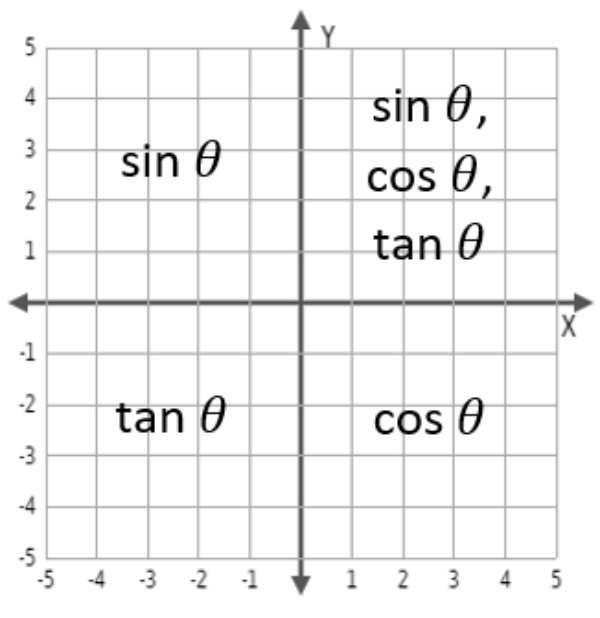
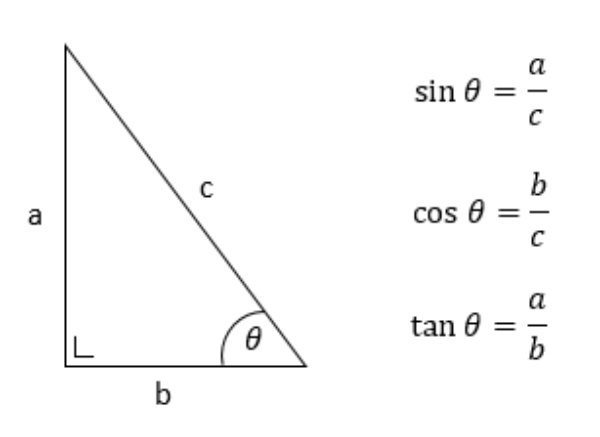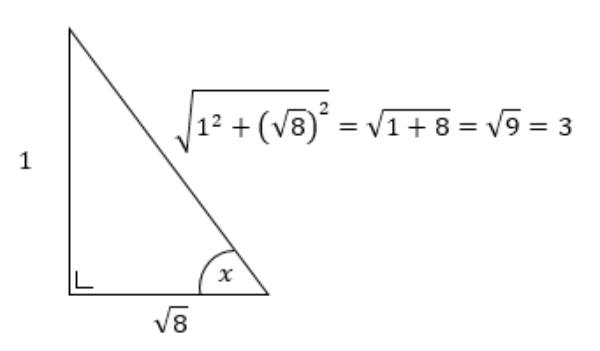Bank Soal Matematika SMA Aplikasi Turunan Fungsi Trigonometri
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Mendorong, membujuk, atau memberikan pengaruh pada banyak orang agar tertarik pada barang atau jasa yang ditawarkan merupakan fungsi dari ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Identifikasi Informasi
Ciri yang menunjukkan Indonesia sebagai negara maritim adalah ....
IPS
Level 5
Geografi
Karakteristik Geografi Wilayah Indonesia
Karakteristik Geografis
Paman mengendarai mobil dengan kecepatan 50 km/jam. Jika paman berangkat pukul 07.30 dan tiba pukul 10.00. Jarak yang ditempuh paman yaitu …
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Kecepatan
Read the following conversation and answer the question.

Mega : Hey! I'm Mega.
Bayu : I'm Bayu. I'm in fifth grade. (1) ...?
Mega : I'm in fifth grade, too. (2) ...?
Bayu : I go to Matahari Elementary School. And you?
Mega : I go to Lentera Elementary School.
What are the appropriate expressions to complete the conversation?
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Self-Introduction
Panjang sisi kubus dengan luas permukaan 1.734 cm2 adalah ... cm
Matematika
Level 5
Geometri
Balok dan Kubus
Luas Permukaan Balok dan Kubus
Diagram di bawah berisikan fluktuasi harga bensin dari bulan Januari hingga bulan Juni.
Berdasarkan diagram di atas, harga bensin mencapai titik tertingginya pada bulan....
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Bacalah teks berikut!
Adat istiadat merupakan suatu sistem norma atau tata kelakuan yang tumbuh, berkembang, dan dijunjung tinggi oleh masyarakat secara turun-temurun. Adat istiadat juga merupakan kebiasaan sosial yang sejak lama telah ada di masyarakat dan bertujuan untuk mengatur tata tertib dalam masyarakat tersebut.
Keberagaman budaya menjadikan adat istiadat beragam pula. Adat istiadat terbentuk sesuai dengan kebiasaan masyarakat setempat. Setiap suku yang ada di Indonesia memiliki adat istiadat yang berbeda. Sebagai contoh, tradisi masyarakat Jawa berbeda dengan masyarakat NTT, Bali, maupun Papua. Adat istiadat memiliki aturan khusus yang mengikat masyarakat. Adat istiadat memiliki nilai budaya yang luhur, bersifat mengikat suatu kelompok masyarakat yang tinggal di daerah tertentu, dan memiliki sistem hukum yang tegas bagi seluruh masyarakat.
Meskipun setiap daerah memiliki adat istiadatnya masing-masing, namun Indonesia harus tetap hidup rukun dan damai. Saling menghormati antar suku dan budaya seperti semboyan Bangsa Indonesia yaitu Bhinneka Tunggal Ika, yang artinya berbeda-beda tetapi tetap satu. Perbedaan juga menjadi sebuah kekuatan sehingga memperkaya sifat budaya bangsa Indonesia serta persatuan dan kesatuan bangsa.
Teks tersebut termasuk jenis eksplanasi ....
Bahasa Indonesia
Level 5
Membaca
Teks Eksplanasi
Informasi Penting dalam Teks
Diketahui data tinggi badan (dalam cm) dari 30 murid kelas VI sebagai berikut.

Berapa cm tinggi badan terendah? Ada berapa orang yang memiliki tinggi badan terendah?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Rumus untuk menghitung volume balok yaitu …
Matematika
Level 5
Geometri
Balok dan Kubus
Volume Balok dan Kubus
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Mendorong, membujuk, atau memberikan pengaruh pada banyak orang agar tertarik pada barang atau jasa yang ditawarkan merupakan fungsi dari ....
Ciri yang menunjukkan Indonesia sebagai negara maritim adalah ....
Paman mengendarai mobil dengan kecepatan 50 km/jam. Jika paman berangkat pukul 07.30 dan tiba pukul 10.00. Jarak yang ditempuh paman yaitu …
Read the following conversation and answer the question.

Mega : Hey! I'm Mega.
Bayu : I'm Bayu. I'm in fifth grade. (1) ...?
Mega : I'm in fifth grade, too. (2) ...?
Bayu : I go to Matahari Elementary School. And you?
Mega : I go to Lentera Elementary School.
What are the appropriate expressions to complete the conversation?
Panjang sisi kubus dengan luas permukaan 1.734 cm2 adalah ... cm
Diagram di bawah berisikan fluktuasi harga bensin dari bulan Januari hingga bulan Juni.
Berdasarkan diagram di atas, harga bensin mencapai titik tertingginya pada bulan....
Bacalah teks berikut!
Adat istiadat merupakan suatu sistem norma atau tata kelakuan yang tumbuh, berkembang, dan dijunjung tinggi oleh masyarakat secara turun-temurun. Adat istiadat juga merupakan kebiasaan sosial yang sejak lama telah ada di masyarakat dan bertujuan untuk mengatur tata tertib dalam masyarakat tersebut.
Keberagaman budaya menjadikan adat istiadat beragam pula. Adat istiadat terbentuk sesuai dengan kebiasaan masyarakat setempat. Setiap suku yang ada di Indonesia memiliki adat istiadat yang berbeda. Sebagai contoh, tradisi masyarakat Jawa berbeda dengan masyarakat NTT, Bali, maupun Papua. Adat istiadat memiliki aturan khusus yang mengikat masyarakat. Adat istiadat memiliki nilai budaya yang luhur, bersifat mengikat suatu kelompok masyarakat yang tinggal di daerah tertentu, dan memiliki sistem hukum yang tegas bagi seluruh masyarakat.
Meskipun setiap daerah memiliki adat istiadatnya masing-masing, namun Indonesia harus tetap hidup rukun dan damai. Saling menghormati antar suku dan budaya seperti semboyan Bangsa Indonesia yaitu Bhinneka Tunggal Ika, yang artinya berbeda-beda tetapi tetap satu. Perbedaan juga menjadi sebuah kekuatan sehingga memperkaya sifat budaya bangsa Indonesia serta persatuan dan kesatuan bangsa.
Teks tersebut termasuk jenis eksplanasi ....
Diketahui data tinggi badan (dalam cm) dari 30 murid kelas VI sebagai berikut.
Berapa cm tinggi badan terendah? Ada berapa orang yang memiliki tinggi badan terendah?
Rumus untuk menghitung volume balok yaitu …