Bank Soal Matematika SMA Aplikasi Turunan Fungsi Trigonometri
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Matematika
Level 3
Bilangan
Pecahan

Keliling bangun pada gambar adalah … cm.
Matematika
Level 6
Geometri
Bangun Datar
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"

Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra

Read the situation and answer the question.
Your father needs somebody to help the company with money problems.
He needs a/an ....
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Vocabulary: Jobs
Faktor persekutuan dari 32 dan 36 adalah …
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Faktor Persekutuan
Poligon yang mempunyai 7 sisi dinamakan?
Matematika
Level 4
Geometri
Bangun Datar
Segi Banyak
KPK dari bilangan 42 dan 56 adalah ...
Matematika
Level 4
Bilangan
FPB dan KPK
KPK
Cermati teks berikut!
Jaka Tarub

Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Cerita Rakyat
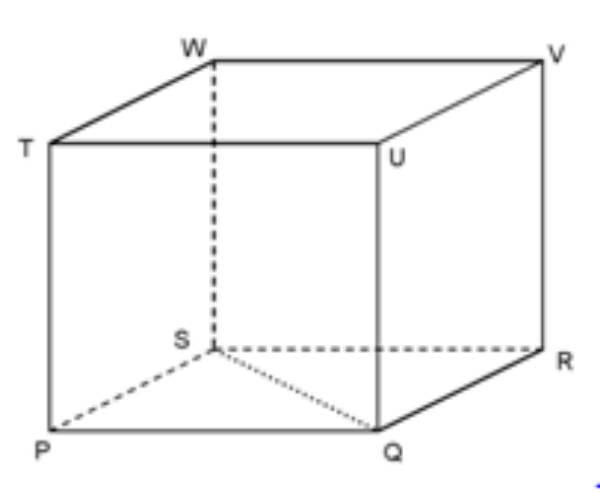
Pada kubus PQRS.TUVW, tentukan kedudukan garis RT dan SU!
Matematika
Level 4
Geometri
Garis dan Sudut
Hubungan Antar Garis
Berikut adalah diagram batang warna kaos dan jumlah kaos yang ada di gudang.
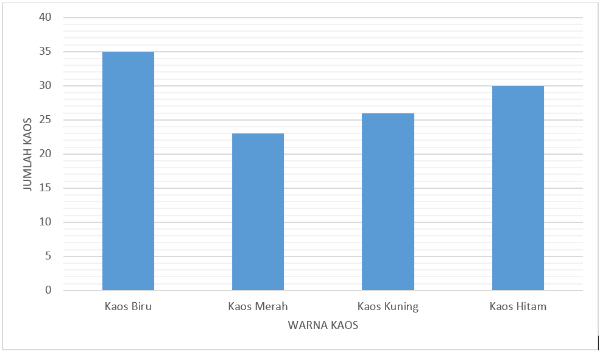
Kaos warna apakah yang mempunyai jumlah paling banyak?
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Keliling bangun pada gambar adalah … cm.
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"
Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....

Read the situation and answer the question.
Your father needs somebody to help the company with money problems.
He needs a/an ....
Faktor persekutuan dari 32 dan 36 adalah …
Poligon yang mempunyai 7 sisi dinamakan?
KPK dari bilangan 42 dan 56 adalah ...
Cermati teks berikut!
Jaka Tarub
Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Amanat yang terdapat pada cerita di atas adalah ....
Pada kubus PQRS.TUVW, tentukan kedudukan garis RT dan SU!
Berikut adalah diagram batang warna kaos dan jumlah kaos yang ada di gudang.
Kaos warna apakah yang mempunyai jumlah paling banyak?



