Bank Soal Matematika SMA Persamaan Trigonometri
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Frekuensi harapan muncul sisi angka pada pelemparan dua buah uang logam adalah 9 kali. Berapa banyak lemparan yang dilakukan?
Matematika
Level 8
Statistika
Peluang
Frekuensi Harapan
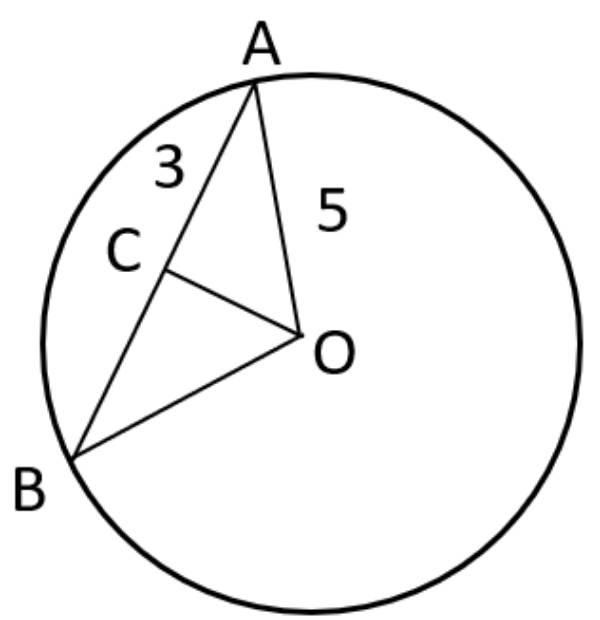
O adalah titik pusat, panjang garis AC adalah 3 cm ,dan AO adalah 5 cm. Jika garis OC adalah apotema, maka panjang garis OC adalah ... cm.
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Perhatikan gambar berikut!
Diketahui panjagn busur AB dan busur BC berturut-turut adalah 33 cm dan 22 cm. Jika luas juring BOC adalah 154 cm2, berapakah luas juring AOB?
Matematika
Level 8
Geometri
Lingkaran
Di antara pasangan titik koordinat berikut ini, yang terletak di kuadran I dan II adalah?
(i) (1, 2) dan (2, 4)
(ii) (2, -3) dan (3, -2)
(iii) (-4, 7) dan (-1, 4)
(iv) (-2, -5) dan (-2, -1)
Matematika
Level 8
Geometri
Koordinat Kartesius
Bacalah paragraf di bawah!
Kebakaran hutan yang terjadi di Kalimantan beberapa pekan lalu kembali terjadi pada Senin (19/02/2020). Diduga kebakaran tersebut terjadi karena adanya oknum-oknum yang sengaja membuang puntung rokok yang masih menyala di dalam hutan. Ranting-ranting kering dan musim kemarau yang tidak kunjung berakhir menambah faktor pendukung penyebab kebakaran hutan kemarin.
Pernyataan yang sesuai dengan paragraf berita di atas adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Simpulan Isi Berita
Kinan — drive — patient — all my friends.
The correct superlative adverb based on the clues is ...
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Di antara titik berikut, manakah yang memiliki tempat kedudukan paling kiri?
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik dan Bangun Datar
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Pola penyajian dan Kebahasaan Iklan, Slogan, Poster
Look at the following picture.

Source: wisdomquotesandstories.com
What will you do if you see this?
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Frekuensi harapan muncul sisi angka pada pelemparan dua buah uang logam adalah 9 kali. Berapa banyak lemparan yang dilakukan?
O adalah titik pusat, panjang garis AC adalah 3 cm ,dan AO adalah 5 cm. Jika garis OC adalah apotema, maka panjang garis OC adalah ... cm.
Perhatikan gambar berikut!
Diketahui panjagn busur AB dan busur BC berturut-turut adalah 33 cm dan 22 cm. Jika luas juring BOC adalah 154 cm2, berapakah luas juring AOB?
Di antara pasangan titik koordinat berikut ini, yang terletak di kuadran I dan II adalah?
(i) (1, 2) dan (2, 4)
(ii) (2, -3) dan (3, -2)
(iii) (-4, 7) dan (-1, 4)
(iv) (-2, -5) dan (-2, -1)
Bacalah paragraf di bawah!
Kebakaran hutan yang terjadi di Kalimantan beberapa pekan lalu kembali terjadi pada Senin (19/02/2020). Diduga kebakaran tersebut terjadi karena adanya oknum-oknum yang sengaja membuang puntung rokok yang masih menyala di dalam hutan. Ranting-ranting kering dan musim kemarau yang tidak kunjung berakhir menambah faktor pendukung penyebab kebakaran hutan kemarin.
Pernyataan yang sesuai dengan paragraf berita di atas adalah ....
Kinan — drive — patient — all my friends.
The correct superlative adverb based on the clues is ...
Di antara titik berikut, manakah yang memiliki tempat kedudukan paling kiri?
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
Look at the following picture.
Source: wisdomquotesandstories.com
What will you do if you see this?



